По определению логарифма.. Метод потенцирования (освобождения от знака логарифма).. Решение уравнений с использованием свойств логарифмов.. Метод введения новой переменной.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

1) По определению логарифма.

По определению логарифма решаются простейшие уравнения вида .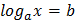

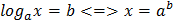Пример 1. Решить уравнение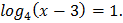

Решение: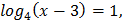

ОДЗ: ,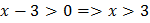

Используем определение логарифма:

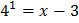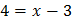Ответ: .

Пример 2. Решить уравнение ,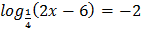

Решение: ,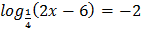

ОДЗ: .

По определению логарифма:

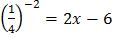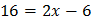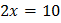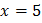Ответ: .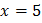

2) Метод потенцирования (освобождения от знака логарифма).

Решение логарифмического уравнения 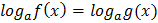основано на том, что данное уравнение равносильно уравнению при дополнительных условиях

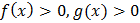Пример 3. Решить уравнение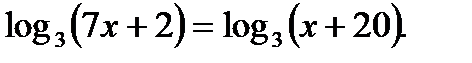

Решение:

ОДЗ: < .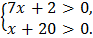

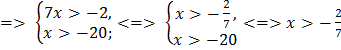Потенцируя получим:

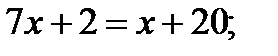
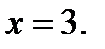
Ответ: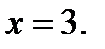

3) Решение уравнений с использованием свойств логарифмов.

Пример 4. Решить уравнение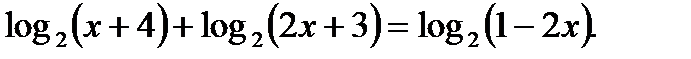

Решение:

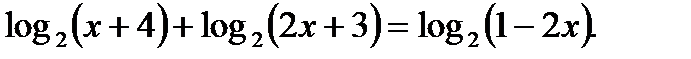
ОДЗ: .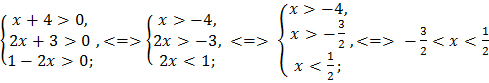

Вспомним свойства логарифмов – сумма логарифмов двух положительных чисел равна логарифму произведения этих чисел, поэтому:

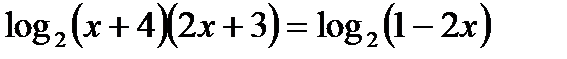
Освободимся от знака логарифма и решим квадратное уравнение:

, .

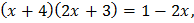
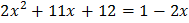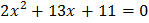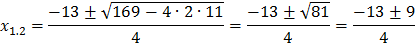
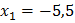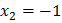Согласовав корни с ОДЗ, получим корень .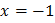

Ответ: .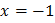

4) Метод введения новой переменной.

Пример 5. Решить уравнение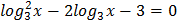

Решение:

ОДЗ: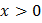

В данном уравнении повторяется выражение: 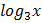. Значит можно выполнить замену переменной.

Пусть 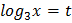. Тогда уравнение примет вид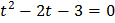

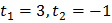
Возвратимся к исходной переменной. Остается решить простейшие логарифмические уравнения:

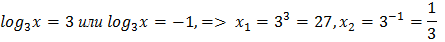
Ответ: .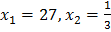

При решении логарифмических уравнений, возможно появление посторонних корней. Причина их появления — расширение области определения исходного уравнения. Поэтому проверка корней логарифмического уравнения осуществляется либо по области определения, либо непосредственной подстановкой найденных корней в исходное логарифмическое уравнение.

Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическими.

⇐ Предыдущая 123 Следующая ⇒