Контакты

Случайная статья

Геометрический смысл определенного интеграла

⇐ ПредыдущаяСтр 2 из 2

Геометрический смысл определенного интеграла

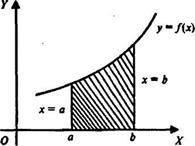
Геометрический смысл определённого интеграла: площадь фигуры, ограниченной кривой у = f (х), где f (х) 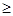0, осью ОХ и двумя прямыми х = а и х = b (рис. 1), выражается

определённым интегралом: S =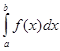

Рис1

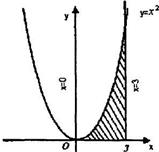
Пример 1:определить площадь S фигуры, заключённой между ветвью кривой у = х², осью ОХ и прямыми х = 0, х = 3 (рис.2).

Решение: S=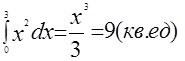

Пример 2:Найти площадь S фигуры, заключённой между осью ОХ и кривой у=х²-4х (рис.3)

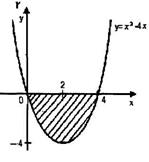
рис. 3

Решение: рассмотрим точки пересечения кривой у = х² - 4х с осью ОХ

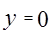
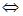х²-4х = 0 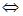х(х-4) = 0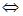 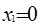или х₂ = 4.

Найдём производную функции 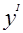= 2х - 4 и точки экстремума:

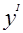= 0 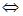2х-4 = 0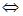^: х = 2^: у" =2>0 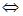х = 2 - точка min y(2) = - 4

Искомая площадь ограничена сверху OX, снизу y = х² – 4x, слева х = 0, справа

х = 4. Так как у < 0, то

S= (x² -4х)dх = 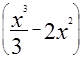= = 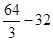= = 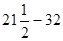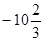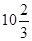(кв. ед.)

Пример 3: Найти площадь фигуры, заключённой между 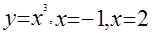и осью OX (рис.4 )

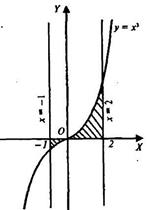
рис. 4

Найдем точки пересечения графика функции 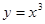с осью абсцисс .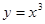

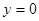
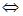
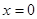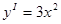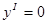
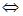
Точки экстремума: ; ; 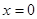; ; 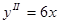; 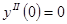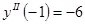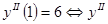меняет знак при переходе через х=0 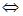т. (0;0) - точка перегиба. Значит, искомая площадь состоит из двух частей:

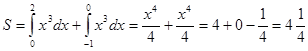(кв.ед.)

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.