
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Алиев. Вариант 3. Асламурзаев. Вариант 4
Алиев
Вариант 3
1. На множестве 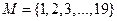 заданы предикаты: A(x): “x – чётное число”; B(х): “x не делится на 5”, С(х): “х кратно 6”. Найти множество истинности предиката
заданы предикаты: A(x): “x – чётное число”; B(х): “x не делится на 5”, С(х): “х кратно 6”. Найти множество истинности предиката 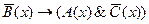 .
.
2. Изобразить на координатной плоскости область истинности предиката  .
.
3. Записать решение неравенства 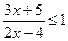 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность предикатов 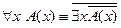 методом конкретизации.
методом конкретизации.
5. Найти отрицание формулы 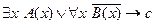 и привести её к предварённой нормальной форме.
и привести её к предварённой нормальной форме.
6. Доказать общезначимость формулы 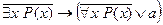 .
.
7. Суждение “Между двумя различными точками на прямой лежит, по меньшей мере, одна, с ними не совпадающая” записать в виде формулы логики предикатов. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Асламурзаев
Вариант 4
1. Предметные переменные в предикатах принадлежат R. Указав области истинности предикатов, установить, являются ли они равносильными или один из них является следствием другого: 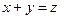 и
и  .
.
2. Изобразить на координатной плоскости область истинности предиката 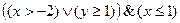 .
.
3. Записать решение уравнения 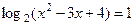 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность предикатов "xA(x) & B º"x(A(x) & B) методом конкретизации.
5. Найти отрицание формулы 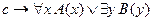 и привести её к предварённой нормальной форме.
и привести её к предварённой нормальной форме.
6. Является ли формула 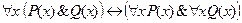 тавтологией?
тавтологией?
7. Даны предикаты: Р(x): "x – простое число"; О(x): "x – нечётное число"; D(x, y): “х делит у” или “у делится на х”. Перевести на естественный язык символическую запись на языке логики предикатов C = 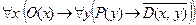 , учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
, учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Берёзов
Вариант 5
1.На множестве 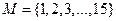 заданы предикаты: B(х): “x не делится на 5”; C(x): “x кратно 3”; D(x): “x – число простое”. Найти множество истинности предиката
заданы предикаты: B(х): “x не делится на 5”; C(x): “x кратно 3”; D(x): “x – число простое”. Найти множество истинности предиката 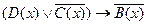 .
.
2. Изобразить на координатной плоскости область истинности предиката 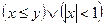 .
.
3. Записать решение неравенства 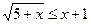 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность предикатов $xA(x) Ú B º$x(A(x) Ú B) методом конкретизации.
5. Найти отрицание формулы 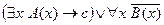 и привести её к предварённой нормальной форме.
и привести её к предварённой нормальной форме.
6.Доказать, что формула 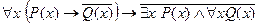 , общезначима.
, общезначима.
7. Суждение “Не всякое действительное число является рациональным” записать в виде формулы логики предикатов. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Бетрозов
Вариант 6
1. На множестве 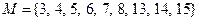 заданы два предиката
заданы два предиката 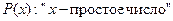 и
и 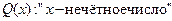 . Составить область истинности предиката
. Составить область истинности предиката 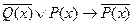 .
.
2. Изобразить на координатной плоскости область истинности предиката 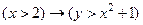 .
.
3. Записать решение уравнения 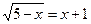 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
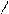 4. Доказать, что $x (A(y) ® Q(x)) A(y) ® "x Q(x) методом конкретизации.
4. Доказать, что $x (A(y) ® Q(x)) A(y) ® "x Q(x) методом конкретизации.
5. Найти отрицание формулы 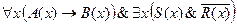 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6. Доказать, что формула 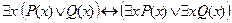 является тавтологией.
является тавтологией.
7. Записать на языке логики предикатов определение возрастающей функции. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Горбатых
Вариант 7
1. На множестве 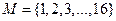 заданы предикаты: B(х): “x делится на 8”; D(x): “x – число простое”. Найти множество истинности предиката
заданы предикаты: B(х): “x делится на 8”; D(x): “x – число простое”. Найти множество истинности предиката 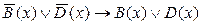 .
.
2.Изобразить на координатной плоскости область истинности предиката 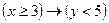 .
.
3. Записать решение неравенства 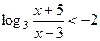 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность 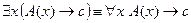 методом конкретизации.
методом конкретизации.
5. Найти отрицание формулы 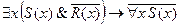 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6. Выполнима ли формула 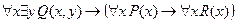 ?
?
7. Суждение “Через две различные точки на плоскости проходит единственная прямая” записать в виде формулы логики предикатов. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Гучмазов
Вариант 8
1. На множестве 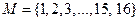 заданы предикаты: B(х): “x делится на 5”; C(x): “x не кратно 3”; D(x): “x – число простое”. Найти множество истинности предиката
заданы предикаты: B(х): “x делится на 5”; C(x): “x не кратно 3”; D(x): “x – число простое”. Найти множество истинности предиката 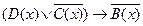 .
.
2. Изобразить на координатной плоскости область истинности предиката 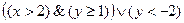 .
.
3. Записать решение уравнения 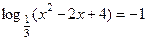 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность предикатов "x (A(x) ® B º $xA(x) ® B методом конкретизации.
5. Найти отрицание формулы 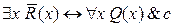 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6. Проверить общезначимость формулы  .
.
7. Данное суждение “Если произведение нескольких натуральных чисел делится на простое число, то на него делится по меньшей мере один из сомножителей” записать в виде формулы логики предикатов. Построить отрицание данного суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Джусоев
Вариант 9
1. На множестве 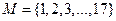 заданы предикаты: A(x): “x – чётное число”; B(х): “x не делится на 4”; D(x): “x – число составное”. Найти множество истинности предиката
заданы предикаты: A(x): “x – чётное число”; B(х): “x не делится на 4”; D(x): “x – число составное”. Найти множество истинности предиката 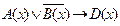 .
.
2.Изобразить на координатной плоскости область истинности предиката 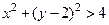 .
.
3. Записать решение неравенства 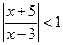 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность 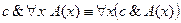 методом конкретизации.
методом конкретизации.
5. Найти отрицание формулы 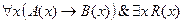 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6. Выполнима ли формула 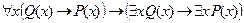 ?
?
7. Записать на языке логики предикатов определение периодической функции. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Кайтуков
Вариант 10
1. Предметные переменные в предикатах принадлежат R. Указав области истинности предикатов установить, являются ли они равносильными или один из них является следствием другого: 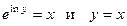 .
.
2. Изобразить на координатной плоскости область истинности предиката  .
.
3. Записать решение уравнения 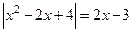 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность предикатов $x (B ®A(x) º B ® $x A(x) методом конкретизации.
5. Найти отрицание формулы 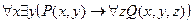 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6. Доказать общезначимость формулы
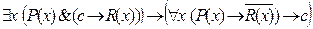 .
.
7. Даны предикаты: О(x): "x – чётное число"; D(x, y): “х делит у” или “у делится на х”. Перевести на естественный язык символическую запись C = 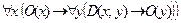 , учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
, учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Калухов
Вариант 11
1.На множестве 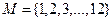 заданы предикаты: B(х): “x не делится на 7”; C(x): “x кратно 3”. Найти множество истинности предиката
заданы предикаты: B(х): “x не делится на 7”; C(x): “x кратно 3”. Найти множество истинности предиката 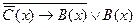 .
.
2. Изобразить на координатной плоскости область истинности предиката 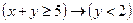 .
.
3. Записать решение неравенства 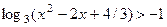 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
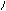 4. Доказать, что
4. Доказать, что 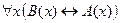 º
º 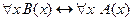 методом конкретизации.
методом конкретизации.
5. Найти отрицание формулы 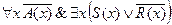 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6. Доказать общезначимость формулы 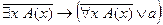 .
.
7. Записать на языке логики предикатов определение монотонной функции. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Карасаев
Вариант 12
1. Найти область истинности предиката 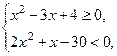 если его область определения N.
если его область определения N.
2. Изобразить на координатной плоскости область истинности предиката 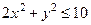 .
.
3. Записать решение уравнения 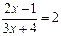 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность "xA(x) & "xB(x) º "x(A(x) & B(x)) методом конкретизации.
5. Найти отрицание формулы 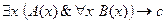 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6. Доказать, что формула 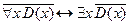 является тавтологией.
является тавтологией.
7. Данное суждение “Через три точки, не лежащие на одной прямой, проходит единственная плоскость” записать в виде формулы логики предикатов. Построить отрицание данного суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Макиев
Вариант 13
1. На множестве 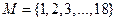 заданы предикаты: A(x): “x – чётное число”; C(x): “x кратно 8”; D(x): “x – число простое”. Найти множество истинности предиката
заданы предикаты: A(x): “x – чётное число”; C(x): “x кратно 8”; D(x): “x – число простое”. Найти множество истинности предиката 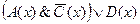 .
.
2. Изобразить на координатной плоскости область истинности предиката 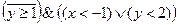 .
.
3. Записать решение неравенства 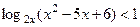 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность 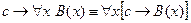 методом конкретизации.
методом конкретизации.
5. Найти отрицание формулы 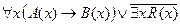 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6.Является формула 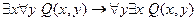 тавтологией?
тавтологией?
7. Даны предикаты: Е(x): "x – чётное число"; D(x, y): “х делит у” или “у делится на х”. Перевести на естественный язык символическую запись C = 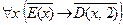 , учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
, учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Тамаев
Вариант 14
1. На множестве 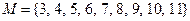 заданы два предиката
заданы два предиката 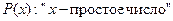 и
и 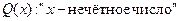 . Составить область истинности предиката
. Составить область истинности предиката 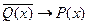 . Равносильны ли предикаты Р(х) и Q(х) на множестве
. Равносильны ли предикаты Р(х) и Q(х) на множестве 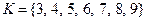 ?
?
2. Изобразить на координатной плоскости область истинности предиката 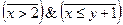 .
.
3. Записать решение уравнения 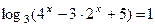 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность 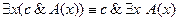 методом конкретизации.
методом конкретизации.
5. Найти отрицание формулы 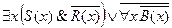 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6. Является ли формула 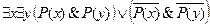 выполнимой?
выполнимой?
7. Суждение “Ни одно четное число, большее 2, не является простым” записать в виде формулы логики предикатов. Построить отрицание данного суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Тандуев
Вариант 215
1.На множестве 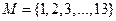 заданы предикаты: B(х): “x делится на 2”; C(x): “x кратно 3”. Найти множество истинности предиката
заданы предикаты: B(х): “x делится на 2”; C(x): “x кратно 3”. Найти множество истинности предиката 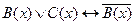 .
.
2. Изобразить на координатной плоскости область истинности предиката 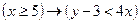 .
.
3. Записать решение неравенства 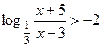 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность $xA(x) Ú $xB(x) º $x(A(x) Ú B(x)) методом конкретизации.
5. Найти отрицание формулы 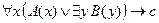 и записать в предварённой форме.
и записать в предварённой форме.
6. Доказать, что формула 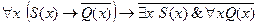 является тавтологией.
является тавтологией.
7. Записать на языке логики предикатов определение чётной функции. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Хестанов
Вариант 16
1. Предметные переменные в предикатах принадлежат R. Указав области истинности предикатов установить, являются ли они равносильными или один из них является следствием другого: 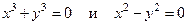 .
.
2. Изобразить на координатной плоскости область истинности предиката 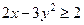 .
.
3. Записать решение уравнения 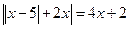 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность 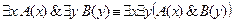 методом конкретизации.
методом конкретизации.
5. Найти отрицание формулы 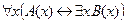 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6. Проверить, является ли выполнимой формула
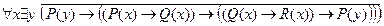 ?
?
7. Даны предикаты: Е(x): "x – чётное число"; D(x, y): “х делит у” или “у делится на х”. Перевести на естественный язык символическую запись C = 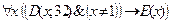 , учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
, учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Хугаев
Вариант 17
1. На множестве 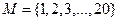 заданы предикаты: A(x): “x – чётное число”; C(x): “x кратно 7”; D(x): “x – число простое”. Найти множество истинности предиката
заданы предикаты: A(x): “x – чётное число”; C(x): “x кратно 7”; D(x): “x – число простое”. Найти множество истинности предиката 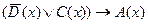 .
.
2. Изобразить на координатной плоскости область истинности предиката 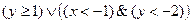 .
.
3. Записать решение неравенства 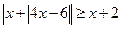 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
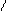 4. Доказать, что
4. Доказать, что 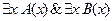 º
º 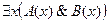 методом конкретизации.
методом конкретизации.
5. Найти отрицание формулы 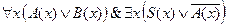 и привести её к предварённой нормальной форме.
и привести её к предварённой нормальной форме.
6. Доказать, что формула 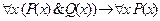 является тавтологией.
является тавтологией.
7. Суждение “Всякий равносторонний треугольник является равнобедренным” записать в виде формулы логики предикатов. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Щур
Вариант 18
1. Найти область истинности предиката 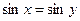 , если его область определения R´R.
, если его область определения R´R.
2. Изобразить на координатной плоскости область истинности предиката 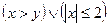 .
.
3. Записать решение уравнения 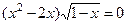 в виде последовательности равносильных предикатов.
в виде последовательности равносильных предикатов.
4. Доказать равносильность  методом конкретизации.
методом конкретизации.
5. Найти отрицание формулы 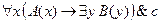 и записать её в предварённой нормальной форме.
и записать её в предварённой нормальной форме.
6. Доказать, что формула 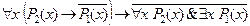 является тавтологией.
является тавтологией.
7. Даны предикаты: А(x): "x – чётное число". Перевести на естественный язык символическую запись на языке логики предикатов C = 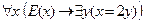 , учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
, учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|