Абисалова. Вариант 1. Алдатов. Вариант 2

Типовой расчёт № 2 по теме: “ЛОГИКА ПРЕДИКАТОВ”

Абисалова

Вариант 1

1. Даны предикаты 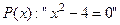и 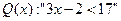. Найти области истинности предиката 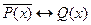, если области определения данных предикатов совпадают и представляют собой N.

2. Изобразить на координатной плоскости область истинности предиката .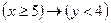

3. Записать решение уравнения 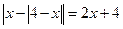в виде последовательности равносильных предикатов.

4. Доказать равносильность предикатов 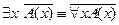методом конкретизации.

5. Найти отрицание формулы и привести её к предварённой нормальной форме.

6. Выполнима ли формула ?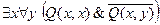

7. Даны предикаты: А(x): "x – простое число"; B(x): "x – чётное число"; D(x, y): “х делит у” или “у делится на х”. Перевести на естественный язык символическую запись на языке логики предикатов C = "x[A(x) ® $у (B(у) & D(x, y))], учитывая, что переменные х и у пробегают множество натуральных чисел. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.

Алдатов

Вариант 2

1. На множестве 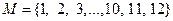заданы предикаты: A(x): “x – чётное число”; D(x): “x – число простое”, В(х): “х не делится на 4”. Найти множество истинности предиката .

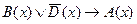2. Изобразить на координатной плоскости область истинности предиката .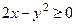

3. Записать решение неравенства 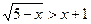в виде последовательности равносильных предикатов.

4. Доказать равносильность предикатов "xA(x) Ú B º"x(A(x) Ú B) методом конкретизации.

5. Найти отрицание формулы 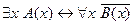и привести её к предварённой нормальной форме.

6. Является ли формула 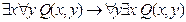тавтологией?

7. Записать на языке логики предикатов определение линейно упорядоченного множества. Построить отрицание этого суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.

12 Следующая ⇒