Геометрические множества некоторых геометрических элементов

⇐ ПредыдущаяСтр 2 из 2

Упражнение

1. На заданной прямой m построить точку, удаленную от точки О на расстояние l (Рисунок 5.1).

Рисунок 5.1

I. Геометрическое решение в пространстве

Искомые точки должны принадлежать прямой m, следовательно, решение по первому условию – любая точка на прямой.
Множество точек, удаленных от точки О на расстояние l образуют в пространстве сферу, с центром в точке О и радиусом равным l.
Общее решение задачи – точки, одновременно принадлежащие прямой m и сфере, то есть точки пересечения прямой m со сферой.

II. Графическое решение задачи (Рисунок 5.2).

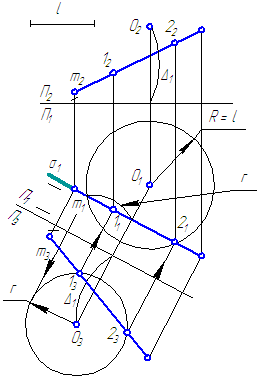
Рисунок 5.2

III. Анализ возможных решений (Рисунок 5.3).

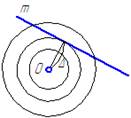
Рисунок 5.3

O∈m;
O∉m;

Обозначим Δ – расстояние от точки О до прямой m:

l > Δ – прямая пересечет сферу в двух точках;
l = Δ – m – касательная к сфере → одна точка;
l < Δ – решения нет.

IV. Краткая запись построения

Строим проекцию сферы с центром в точке О и радиусом l.
Через прямую m проводим секущую плоскость, например, σ⊥π₁. Плоскость σ пересекает сферу, в сечении – окружность.
Вводим ДПП π₃⊥π₁ и π₃//σ.
Строим на π₃ проекции прямой m и окружности сечения, определяем точки пересечения прямой с окружностью, которые являются искомыми.

Упражнение

2. В плоскости σ=ΔАВС через точку А провести прямую AD, удаленную от точки О на расстояние l (О∈σ) (Рисунок 5.4).

I. Геометрическое решение в пространстве

Прямая AD, удаленная от точки О на расстояние l, является касательной к сфере радиусом R_сф = l с центром в точке О.
Прямая AD∈σ.

Плоскость σ пересекает сферу по окружности.

Искомая прямая AD – касательная к окружности сечения плоскости σ и сферы.

II. Графическое решение задачи

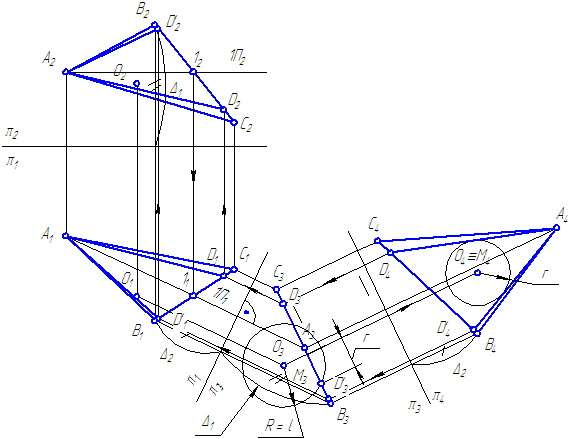
Рисунок 5.4

III. Анализ возможных решений

Обозначим Δ – расстояние от точки О до плоскости σ:

l > Δ – плоскость пересечет сферу по окружности, → две прямые, проходящие через точку А и касательные к окружности сечения (если точка А вне окружности);
если точка А на окружности сечения – одна прямая; если точка А внутри окружности сечения – решения нет;
l = Δ – плоскость касается сферы → одна прямая, проходящая через точку А и точку касания;
если точка А совпала с точкой касания → бесконечное множество прямых принадлежащих плоскости σ;
l < Δ – решения нет.

IV. Краткая запись построения

Находим истинную величину треугольника АВС, например, с помощью введения ДПП:

π₃⊥π₁ и π₃⊥σ.
π₄⊥π₃ и π₄//σ.
Строим окружность сечения σ со сферой. Строим касательные к этой окружности, проходящие через точку А.

5.3. Задачи для самостоятельной работы

1. Задана плоскость α=∆АВС и прямая m – общего положения. Определить угол между прямой m и плоскостью α.
2. Задана плоскость α=∆АВС и точка D вне плоскости. Повернуть точку D так, чтобы она совпала с плоскостью α. Ось вращения i⊥π₁.
3. Продолжите заполнение таблицы, определяя геометрические множества точек, прямых и плоскостей для заданных условий:

Геометрические множества некоторых геометрических элементов

ГМ точек

ГМ прямых

ГМ плоскостей

6. Равноудаленных от двух пересекающихся прямых

…

7. Равноудаленных от двух параллельных плоскостей.

…

8. Равноудаленных от двух пересекающихся плоскостей.

…

⇐ Предыдущая 12