Метод конечных разностей решения линейной двухточечной краевой задачи для ОДУ второго порядка.

1.Метод конечных разностей решения линейной двухточечной краевой задачи для ОДУ второго порядка.

Цель: Описать постановку линейной двухточечной краевой задачи для ОДУ второго порядка с разными граничными условиями. Описать метод конечных разностей для решения этой задачи. Решить в MathCAD краевую задачу для одномерного стационарного уравнения теплопроводности

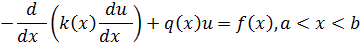
(вид функций k(x), q(x), f(x) выбрать самостоятельно) c точностью 10^-4. Оценить погрешность по Рунге. Построить график решения и график погрешности. Рассмотреть различные краевые условия.

Литература:

Б.П. Демидович, И.А. Марон, Э.З. Шувалова, Численные методы анализа

А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова, Вычислительные методы для инженеров.

Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль

2.Решение линейной двухточечной краевой задачи для ОДУ второго порядка методом Галеркина.

Цель: Описать постановку линейной двухточечной краевой задачи для ОДУ второго порядка с разными граничными условиями. Описать метод Галеркина. Решить в MathCAD краевую задачу. Построить график решения и график невязки. Найти точное решение. Построить график.

Литература:

Б.П. Демидович, И.А. Марон, Э.З. Шувалова, Численные методы анализа.

А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова, Вычислительные методы для инженеров.

3.Метод стрельбы для решения двухточечной краевой задачи для системы дифференциальных уравнений первого порядка.

Цель: Описать постановку линейной двухточечной краевой задачи для системы дифференциальных уравнений первого порядка.Описать метод. Решить в MathCAD систему методом стрельбы . Для определения угла вылета использовать метод Стеффесена. Построить график решения.

Литература:

Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль.

А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова, Вычислительные методы для инженеров.

Дж. Ортега, У.Пул Введение в численные методы решения дифференциальных уравнений.

12 Следующая ⇒