Хелпикс

Главная

Контакты

Случайная статья



Наибольшее и наименьшее значение функции в замкнутой области. Глобальный экстремум.

⇐ ПредыдущаяСтр 2 из 2


§ 8. Наибольшее и наименьшее значение функции в замкнутой области. Глобальный экстремум.

 

Постановка задачи. ____________________________________________________________

_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Алгоритм нахождения наибольшего и наименьшего значения.

1)_________________________________________________________________________________________________________________________________________________________________________________

2)_________________________________________________________________________________________________________________________________________________________________________________

3)______________________________________________________________________________________________________________________________________________________________________________

4)_______________________________________________________________________________________________________________________________________________________________________________

5)_________________________________________________________________________________________________________________________________________________________________________________

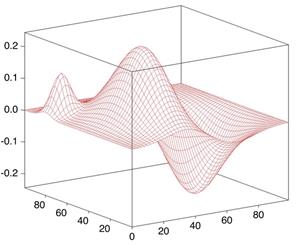
Пример.  Найти наибольшее и наименьшее значения функции 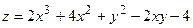 в замкнутой области, ограниченной линиями: , .

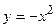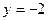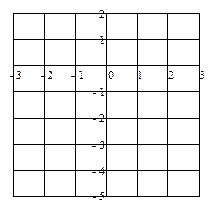Решение.

1) Находим производные первого порядка.

                                                     

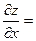
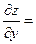
Находим критические точки. Для этого решим систему уравнений:

                                                                                                                       

 

 

Получаем критические точки: _______________________

 

2) Вычисляем значение функции в критических точках внутри области D. Для наглядности нарисуем область D в декартовой системе координат Оху.

____________________________________________________________________________

____________________________________________________________________________

3) Находим критические точки на границе области.

а) исследуем границу 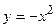 области D.                          

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

 

б) исследуем границу 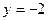 области D.

 

Получаем критические точки: _______________________

 

4) Вычисляем значение функции в критических точках на границе области D.

                                  

 

Вывод: ________________________________________________

 

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

 

 

§ 9. Производная сложной функции. Полная производная.

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Теорема. _________________________________________________________________________________

__________________________________________________________________________________________________________________________________________________________________________________

                                                                                                                                                        

                                                                                      __________________

 

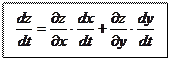
Теорему принимаем без доказательств.

Частный случай теоремы. ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________

_                                     _____________     

 

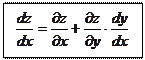
Формула (…) носит название _______________________________

 

Общий случай теоремы.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

_                                     

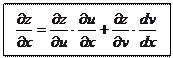
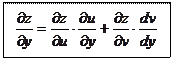Аналогично

 

                                                                    

 

 

§ 10. Исследование функции на условный экстремум (для случая двух переменных)

 

       Функция 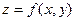имеет условный максимум (минимум) в точке 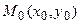, если существует такая окрестность точки 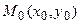, что для всех точек из этой окрестности, удовлетворяющих условию 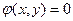, выполняется неравенство 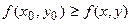(или ).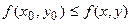

       Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа 

.

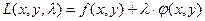Здесь 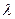называется множителем Лагранжа.

       Необходимые условия условного экстремума функции двух переменных выражаются системой трёх уравнений:

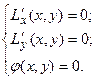                                                     (6)

       Пусть дана точка 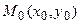 и имеем  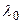- любое из решений этой системы. Составим следующий определитель:

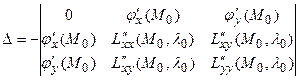.                                     (7)

       Тогда, если 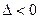, то функция 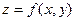имеет в точке 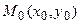условный максимум, если 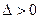, то функция 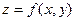имеет в точке 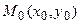условный минимум.

 

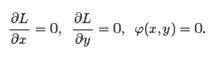Пример.Исследовать функцию  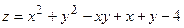на условный экстремум при условии .

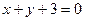Решение.Составим функцию Лагранжа:

.

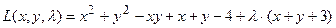Получаем:

;         .

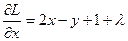Система (6) принимает вид:

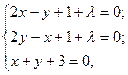или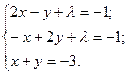

 

Решим систему методом Крамера.

 

;    ;

; .

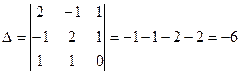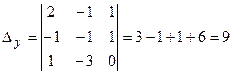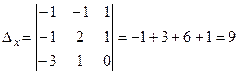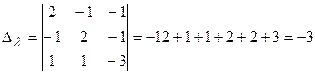Отсюда получаем:

; ; .

 

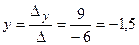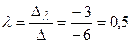Координаты критической (стационарной) точки: .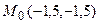

 

Находим вторые производные функции Лагранжа:

;              ;             .

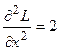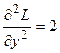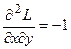Кроме того:     

;                 .

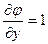Тогда определитель (7):

.

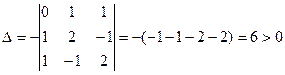Следовательно, в точке 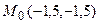 функция  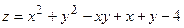имеет условный минимум. Вычислим значения этого минимума:

.

 

 


⇐ Предыдущая12
  

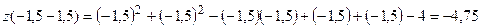© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.