Хелпикс

Главная

Контакты

Случайная статья



Экстремум функции двух переменных.

Стр 1 из 2Следующая ⇒


  § 7. Экстремум функции двух переменных.

Окрестность точки______________________________________

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________


Определение максимума функции двух переменных_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

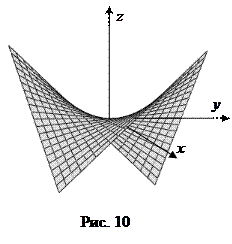
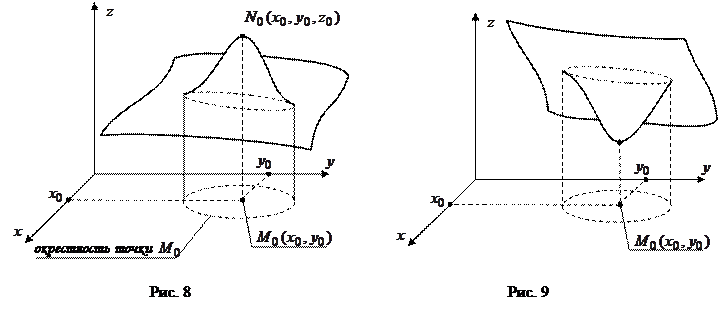Определение минимума функции двух переменных._________________ _______

_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________



Определение экстремума._______________________________________________________ _______________________________________________________________________________________

Теорема (необходимое условие экстремума)__________________________________________

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Принимаем без доказательств.

 

Необходимое условие экстремума не является достаточным (!)

 Пример.Рассмотрим функцию 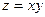 (рис. 10).

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определение критической (стационарной) точки второго рода ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

 

Для ответа на вопрос, является ли точка области определения функции точкой экстремума, нужно использовать достаточное условие экстремума.

Теорема (достаточное условие экстремума)__________________________________________

_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Пример 1.  Исследовать на экстремум функцию .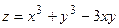

Решение.

1) Находим производные первого порядка.

                                                     

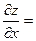
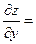
2) Находим критические точки. Для этого решим систему уравнений:

 

Получаем две критические точки: __________________

3) Находим производные второго порядка:

                                                                                             

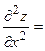
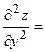
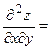
4) Исследуем первую критическую точку:

                                                                

 

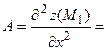
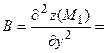
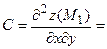
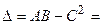
Следовательно, ________________________________________________

 

 

 

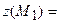
5) Исследуем вторую критическую точку:

                                                                

 

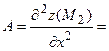
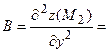
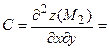
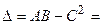
Следовательно, ________________________________________________

Пример 2.  Исследовать на экстремум функцию .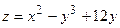

Решение. (самостоятельно)

1) Находим производные первого порядка.

                                                     

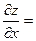
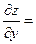
2) Находим критические точки. Для этого решим систему уравнений:

 

Получаем две критические точки: __________________

3) Находим производные второго порядка:

                                                                                             

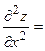
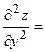
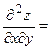
4) Исследуем первую критическую точку:

                                                                  

 

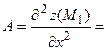
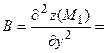
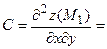
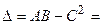
Следовательно, ________________________________________________

 

5) Исследуем вторую критическую точку:

                                                                  

 

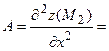
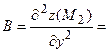
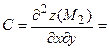
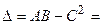
Следовательно, ________________________________________________

 

 


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.