y – x > A) ∨ (x + 4y > 40) ∨ (y – 2x < –35)

ЗАДАЧА 15.

1) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула

(ДЕЛ(x, 5940) Ù ДЕЛ(x, А) Ù ДЕЛ(x, 6300)) ® (ДЕЛ(x, 5940) Ú ДЕЛ(x, A))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

2) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула

((ДЕЛ(x, 12) Ú ДЕЛ(x, 36)) ® ДЕЛ(x, A)) Ù ( A² – A – 90 < 0)

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

3) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула

ДЕЛ(x, A) Ù (A < 10) Ú ДЕЛ(x, 44) Ù ДЕЛ(x, 99) Ù (A < 10)

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

4) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула

((ДЕЛ(x, A) Ù ДЕЛ(x, 180)) ® ДЕЛ(x, 130)) Ù ( A < 100)

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

5) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа A формула

(ДЕЛ(x, A) ® ДЕЛ(x, 54) Ú ДЕЛ(x, 130)) Ù ( A > 110)

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

6) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула

ДЕЛ(120, A) /\ ((ДЕЛ(x, A) /\ ДЕЛ(x, 18)) → ДЕЛ(x, 24))

тождественно истинна, то есть принимает значение 1 при любом натуральном х?

7) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула

ДЕЛ(190, A) /\ ((ДЕЛ(x, A) /\ ДЕЛ(x, 15)) → ДЕЛ(x, 75))

тождественно истинна, то есть принимает значение 1 при любом натуральном х?

8) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа A формула

(ДЕЛ(x, A – 21) 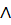ДЕЛ(x, 40 – A)) → ДЕЛ(x, 90)

тождественно истинна, то есть принимает значение 1 при любом натуральном х?

9) Укажите наибольшее целоезначение А, при котором выражение

(y – x > A) ∨ (x + 4y > 40) ∨ (y – 2x < –35)

12 Следующая ⇒