Определенный интеграл как площадь криволинейной трапеции

Определенный интеграл как площадь криволинейной трапеции

Рассмотрим на плоскости прямоугольную систему координат Oty , ось абсцисс которой в данном разделе будем обозначать Ot , а не Ox (рис. 1).

Рис.1

Пусть y = f (t) – непрерывная на отрезке [a, b] функция, принимающая только положительные значения.

Определение 1. Фигуру, ограниченную графиком функции y = f (t) сверху, отрезком [a, b] снизу, а справа и слева отрезками прямых t = a и t = b (рис. 2), называют криволинейной трапецией.

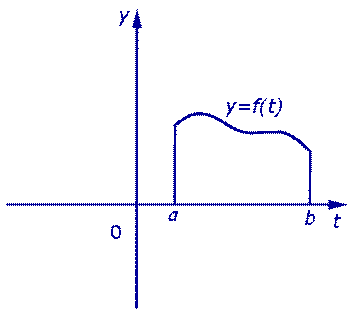
Рис.2

Определение 2. Число, равное площади криволинейной трапеции, изображенной на рисунке 2, называют определенным интегралом от функции f (t) в пределах от a до b и обозначают

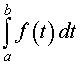
(1)

Формула (1) читается так: «Интеграл от a до b от функции f (t) по dt»

Определение 3. В формуле (1) функцию f (t) называют подынтегральной функцией, переменную t называют переменной интегрирования, отрезок [a, b] называют отрезком интегрирования, число b называют верхним пределом интегрирования, а число a – нижним пределом интегрирования.

Производная от определенного интеграла по верхнему пределу

Если обозначить S (x) площадь криволинейной трапеции, ограниченной с боков отрезками прямых t = a и t = x (рис. 3),

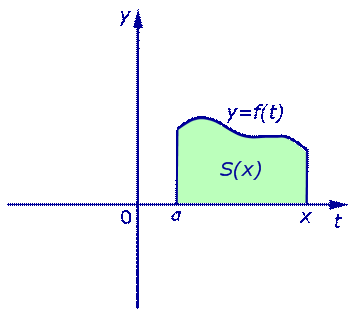
Рис.3

то будет справедлива формула

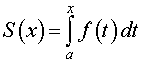
(2)

Теорема 1. Производная от определенного интеграла по верхнему пределу интегрирования равна значению подынтегральной функции в верхнем пределе интегрирования.

12 Следующая ⇒