ПОВТОРЕНИЕ. Тема прошлого урока: Дифференциальные уравнения, в которых переменные уже разделены

ПОВТОРЕНИЕ. Тема прошлого урока: Дифференциальные уравнения, в которых переменные уже разделены

Дифференциальные уравнения, в которых выражение, зависящее от y, входит только в левую часть, а выражение, зависящее от x - только в правую часть, это дифференциальные уравнения с разделенными переменными, в которых переменные уже разделены.

В левой части уравнения может находиться производная от игрека и в этом случае решением дифференциального уравнения будет функция игрек, выраженная через значение интеграла от правой части уравнения.

Пример такого уравнения .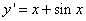

В левой части уравнения может быть и дифференциал функции от игрека и тогда для получения решения уравнения следует проинтегрировать обе части уравнения. Пример такого уравнения .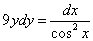

Пример 1. Найти общее решение дифференциального уравнения

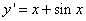
Решение. Пример очень простой. Непосредственно находим функцию по её производной, интегрируя:

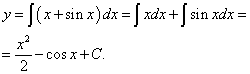
Таким образом, получили функцию - решение данного уравнения.

Пример 2. Найти общее решение дифференциального уравнения

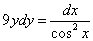
Решение. Интегрируем обе части уравнения:

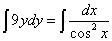Оба интеграла - табличные. Идём к решению:

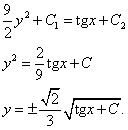
Функция - решение уравнения - получена. Как видим, нужно только уверенно знать табличные интегралы и неплохо расправляться с дробями и корнями.

12 3 4 Следующая ⇒