Контакты

Случайная статья

ЛЕКЦИЯ № 7. Основные теоремы операционного исчисления. Пример 1. Найти свертку функций и .. Решение. Так как , запишем. Решение. 1. Интеграл в левой части уравнения представляет собой свертку функций и . Запишем данное уравнение в виде

Стр 1 из 2Следующая ⇒

ЛЕКЦИЯ № 7

1.Основные теоремы операционного исчисления

●Есл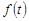и и 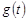– оригиналы, то их сверткой называется функция

.

●Функци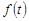и и 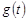называются компонентами свертки.

Пример 1. Найти свертку функций и .

Решение. Так как , запишем

.◄

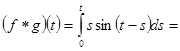
1.Теорема о свертке. Если 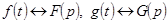, то .

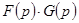Пример 1. Найти оригинал, отвечающий изображению

.

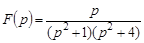Решение.Представим данную функцию 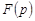в виде произведения двух изображений с известными оригиналами

.

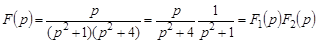Так как

, ,

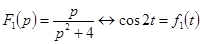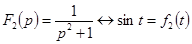то по теореме о свертке

.

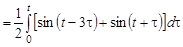
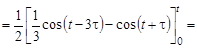
Итак, .◄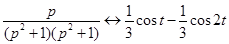

С помощью теоремы о свертке можно находить решение некоторых интегральных уравнений.

Пример 2. Решить интегральные уравнения

1. 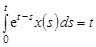, 2. .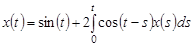

Решение. 1. Интеграл в левой части уравнения представляет собой свертку функций и . Запишем данное уравнение в виде

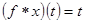
и применим теорему о свертке

.

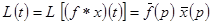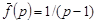Учитывая, что и , получим

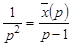и .

Таким образом, решением данного уравнения является функция .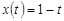

2. Положим 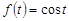и перепишем уравнение в виде

.

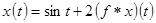Переходя к изображениям и используя теорему о свертке, получим

.

Тогда

.◄

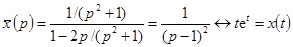2.Теорема о дифференцировании изображения. Если 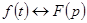, то

;

.

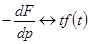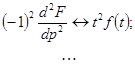
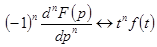Пример 3.Найти изображение функции .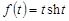

Решение. Для нахождения изображения данной функции воспользуемся теоремой о дифференцировании изображения. Так как 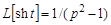, то

◄

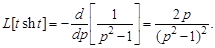Пример 4.Найти изображение функции .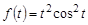

Решение. Имеем

.

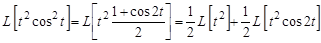Так как, то

.

Изображение функции получим по теореме о дифференцировании изображения:

.

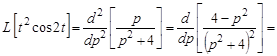
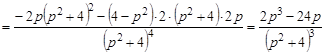Окончательно .◄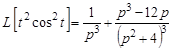

3.Теорема об интегрировании изображения.Если 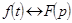, то .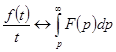

Пример 5.Найти изображение функции .

Решение.Имеем

◄

12 Следующая ⇒

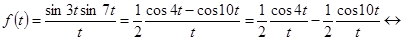
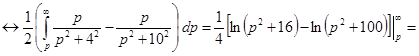
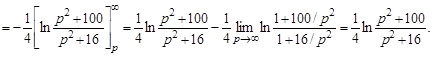© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.