Важные несобственные интегралы первого рода

Важные несобственные интегралы первого рода

1. Интеграл Эйлера-Пуассона (Гауссов интеграл)

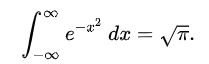
2. Интеграл Дирихле

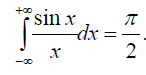
Несобственные интегралы второго рода

Определение:Пусть функция y = f(x) определена на конечном промежутке [a, b] и интегрируема на любом отрезке [a, b – ε], ε < 0, [a, b – ε] ⸦ [a, b). Несобственным интегралом второго роданазывается предел

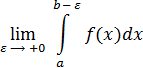
если он существует.

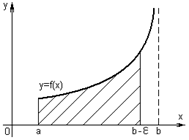
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, а если не существует или бесконечен, то несобственный интеграл – расходящийся.

Обозначение:такое же, как и для определенного интеграла

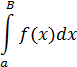
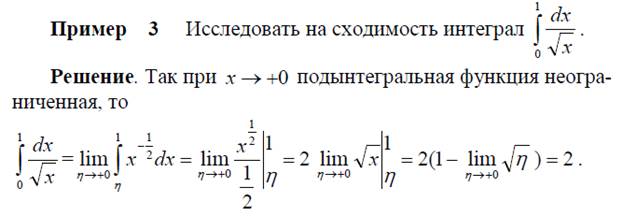
Пример 4

= = = = + = + = + = + = + = ∞ + ∞

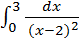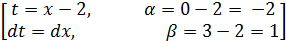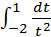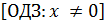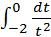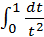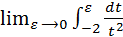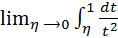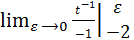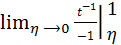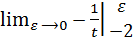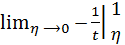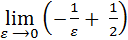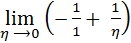Интеграл расходится.

Пример 5

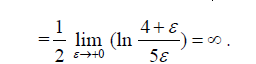
Интеграл расходится.

Домашнее задание:

1, №. 10.237, 10.322; 2, с. 71 – 75.

Литература по теме:

1. Сборник задач и упражнений по высшей математике для студентов экономических специальностей: в 2 ч. / Л.Н.Гайшун, Н.В.Денисенко, А.В.Марков (и др.). – Минск: БГЭУ, 2014. – Ч.2. – 270 с.

2. Шилкина, Е. И. Высшая математика: Часть 2. Учеб.-практ. пособие / Е. И. Шилкина, М. П. Дымков, В. А. Рабцевич. – Мн. : БГЭУ, 2014. – 167 с.

⇐ Предыдущая 12