
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Несобственные интегралы. Несобственные интегралы первого рода
Тема: Несобственные интегралы
До сих пор мы рассматривали определенные интегралы 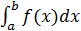 только при выполнении двух условий:
только при выполнении двух условий:
1) промежуток [a, b] конечен;
2) функция f(x) ограничена на этом промежутке.
Если хотя бы одно из этих условий не выполняется, то определенный интеграл нельзя найти по тому определению, которое давалось раннее: бесконечный отрезок нельзя разбить на n отрезков конечной длины; если функция растет до бесконечности, нет предела интегральных сумм.
Тем не менее, интегралы с бесконечностями используются в математике и технике. Их называют неопределенными интегралами. Если бесконечен промежуток интегрирования, перед нами интегралы первого рода. Когда бесконечна функция, мы имеем дело с интегралом второго рода.
Геометрический смысл несобственного интеграла: сходящийся несобственный интеграл означает, что площадь бесконечной фигуры есть конечное число.
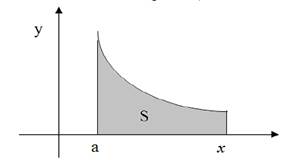
Несобственные интегралы первого рода
Определение: Пусть функция y = f(x) определена на промежутке [a, + ∞] и на любом конечном отрезке [a, B], a < B, B < + ∞ функция y = f(x) интегрируема, то есть существует интеграл 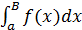 . Тогда несобственным интегралом первого рода (интегралом по бесконечному промежутку)называется предел
. Тогда несобственным интегралом первого рода (интегралом по бесконечному промежутку)называется предел
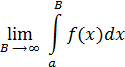
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, а если не существует или бесконечен, то несобственный интеграл – расходящийся.
Аналогично определяются интегралы, у которых бесконечен нижний предел интегрирования или оба предела интегрирования:
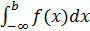 =
= 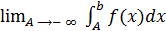
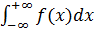 =
= 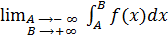
Обозначение: 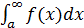 ,
, 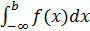 ,
, 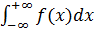
Пример 1. Найти несобственный интеграл
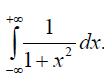
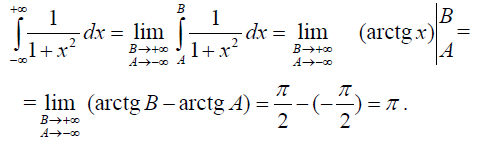

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|