Решить самостоятельно.. Решить самостоятельно.

Решить самостоятельно.

1) Доказать, что решением дифференциального уравнения y´´´ = 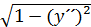является функция y = − sin x + 2x + C.

2) Доказать, что функция y = 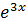является решением дифференциального уравнения y´´´ − 3y´ − 18y = 0.

Определение: Общим решением дифференциального уравнения называется решение вида y = φ(x, C₁, C₂, …, C_n), которое содержит столько независимых произвольных постоянных C₁, C₂, …, C_n, каков порядок этого уравнения.

Общее решение, заданное в неявной форме Φ(x, y, C₁, C₂, …, C_n) = 0 называется общим интегралом уравнения.

Начальные условия – дополнительные условия, которые позволяют рассчитать C₁, C₂, …, C_n. Дополнительные условия – это значения функции и ее производных в конкретной точке (x₀, y₀).

Нахождение решения y = φ(x), удовлетворяющего начальным условиям, называется решением задачи Коши для заданных начальных условий. Решение задачи Коши для заданных начальных условий называется частным решением дифференциального уравнения.

Решить самостоятельно.

1) Установить, является ли функция x² − y² − Cx = 0 общим интегралом дифференциального уравнения 2xyy´ + x² − y² = 0.

2) Показать, что функция y = x² + C является решением дифференциального уравнения y´ = 2x. Построить семейство интегральных кривых и выделить интегральную кривую, проходящую через точку (2; 3).

3) Проинтегрировать дифференциальное уравнение y´´ = 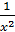. Найти частное решение, удовлетворяющее начальным условиям: y(1) = 0, y´(1) = 1.

Домашнее задание:

1, с. 149 – 153, решить 11.2.б), 11.4.а); 2, с. 76 – 79.

Литература по теме:

1. Сборник задач и упражнений по высшей математике для студентов экономических специальностей: в 2 ч. / Л.Н.Гайшун, Н.В.Денисенко, А.В.Марков (и др.). – Минск: БГЭУ, 2014. – Ч.2. – 270 с.

2. Шилкина, Е. И. Высшая математика: Часть 2. Учеб.-практ. пособие / Е. И. Шилкина, М. П. Дымков, В. А. Рабцевич. – Мн. : БГЭУ, 2014. – 167 с.

⇐ Предыдущая 12