Тема: Дифференциальные уравнения (дифуры)

Тема: Дифференциальные уравнения (дифуры)

Определение: Обыкновенным дифференциальным уравнением n-го порядка называется выражение вида F(x, y, y´, y´´, … y⁽ⁿ⁾), где F – некоторая функция, х – независимая переменная, y(x) – функция, которую требуется найти, y´ – первая производная этой функции, и так далее.

Порядок уравнения – порядок старшей из входящих в него производных.

Дифференциальным уравнением в нормальной форменазывается уравнение вида

y⁽ⁿ⁾ = f (x, y, y´, y´´, … y⁽ⁿ^{- 1)}).

Такое уравнение разрешимо относительно старшей производной.

Пример:

1. y´ − (2xy´) – ln y´ = 0 – обыкновенное дифференциальное уравнение первого порядка.

2. y´´´ = 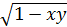– обыкновенное дифференциальное уравнение третьего порядка в нормальной форме;

3. 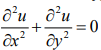– уравнение второго порядка в частных производных.

Решить самостоятельно.Определить порядок дифференциального уравнения:

1) y⁽⁴⁾ – 2y´ + 4 = 0;

2) y´´ + xy´ – x² = 0;

3) y´ – x²y = 0.

Определение: Решение дифференциального уравнения – всякая функция y(x), непрерывная и дифференцируемая на промежутке (a, b), которая обращает уравнение в верное равенство.

Всякому решению на плоскости соответствует кривая, которая называется интегральной кривой дифференциального уравнения.

Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.

12 Следующая ⇒