
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
СТАТИСТИКА
1. СТАТИСТИКА
1.1. Выборочный ряд.Интервалы группировки.
Предметом математической статистики является суждение ослучайной величине X по результатам эксперимента, многократных однотипных наблюдений, в которых фиксируются определенные значения этой случайной величины.
Выборкой объемаn называют совокупность 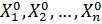 … независимых измерений случайной величины X. При этом говорят, что выборка взятаиз генеральной совокупностиX.
… независимых измерений случайной величины X. При этом говорят, что выборка взятаиз генеральной совокупностиX.
Значения признака, которые при переходе от одного элемента совокупности к другому изменяются, называются вариантами и обозначаются маленькими латинскими буквами.Ряд значений признака, расположенный в порядке возрастания или убывания с соответствующими им весами, называется вариационным рядом.В качестве весов выступают частоты или относительные частоты.Частота (mi)показывает, сколько раз встречается тот или иной вариант в статистической совокупности.Относительная частота (wi) показывает, какая часть единиц совокупности имеет тот или иной вариант к сумме всех частот ряда. Относительная частота рассчитывается по формуле 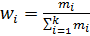 .
.
Вариационные ряды могут быть представлены в дискретной и интервальной форме.Дискретные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга не менее чем на некоторую конечную величину (задаются точечные значения признака, см. Табл.1).
Таблица 1. Общий вид дискретного ряда
| Значения признака (хi) | х1 | х2 | … | хk |
| Частоты (mi) | m1 | m2 | … | mk |
В интервальных вариационных рядах значения признаков в них задаются в виде интервалов (см. Табл.2).
Таблица 2. Общий вид интервального ряда
| Значения признака (хi) | (a1; a2] | (a2; a3] | … | (ai-1;ai] |
| Частоты (mi) | m1 | m2 | … | mi |
Разность между верхней и нижней границами интервала называется интервальной разностью или длиной интервала. В общем виде интервальную разность kiможно представить какki= xi (max) - xi (min).Если интервалы в вариационных рядах имеют одинаковую длину, их называют равновеликими.
Для определения оптимальной величины интервалов применяют формулу Стерджессаn=1+[log2N], где n- количество интервалов, N–общее число наблюдений.
1.2. Гистограмма и полигон
Гистограмма – это ступенчатая фигура, состоящая из прямоугольников, основания которых – интервалы длины h, а высоты - 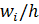 , т. е. площадь каждого прямоугольника равна соответствующей относительной частоте,а полная площадь всей гистограммы равна единице.
, т. е. площадь каждого прямоугольника равна соответствующей относительной частоте,а полная площадь всей гистограммы равна единице.
При большом числе наблюдений и увеличении количества интервалов контур гистограммы приближается к графику функции плотности вероятности и по виду гистограммы можно предварительно сделать вывод о законе распределения изучаемой непрерывной изучаемой величины.
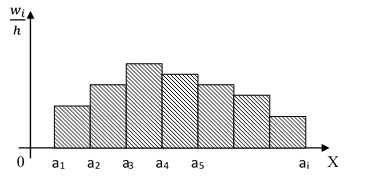
Рис.1.Гистограмма
Полигоном относительных частот называют ломаную, отрезки которойсоединяют точки 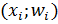 , где xi- середины интервалов, wi– соответствующиеим относительные частоты. По виду полигона можно выдвинутьгипотезу о законе распределения дискретной случайной величины.
, где xi- середины интервалов, wi– соответствующиеим относительные частоты. По виду полигона можно выдвинутьгипотезу о законе распределения дискретной случайной величины.
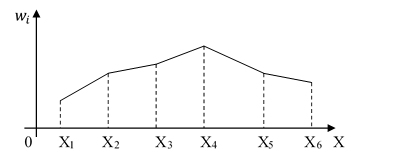
Рис.2. Полигон частот
1.3. Эмпирическая функция распределения
Эмпирическая функция распределения (или кумулянта) определяется следующим равенством: 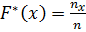 , где nx- число выборочных значений X, меньших x. При увеличении числа наблюдений график
, где nx- число выборочных значений X, меньших x. При увеличении числа наблюдений график 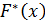 приближается к графику функции распределенияизучаемой случайной величины. Таким образом график эмпирической функциираспределения позволяет выдвинуть гипотезу о виде распределения.
приближается к графику функции распределенияизучаемой случайной величины. Таким образом график эмпирической функциираспределения позволяет выдвинуть гипотезу о виде распределения.
1.4. Основные числовые выборочные характеристики
Выборочным начальным моментом k-го порядка называют величину mk, вычисляемую по формуле 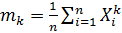 .
.
Выборочный момент 1-го порядка обозначают 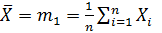 и называют выборочным средним.
и называют выборочным средним.
Выборочным центральным начальным моментом k-го порядка называют величину vk, вычисляемую по формуле 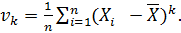
При k=2получаем выборочную дисперсию 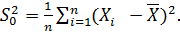
Так как эта оценка оказывается смещенной, рассматривают так называемую исправленную выборочную дисперсию: 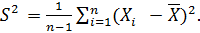
Пусть имеются две выборки одинакового объема 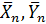 , тогда для них может быть найден выборочный корреляционный момент
, тогда для них может быть найден выборочный корреляционный момент
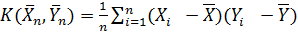 .
.
Выборочным коэффициентом корреляции называют величину
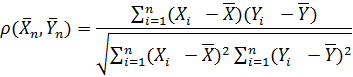
Задачи для самостоятельного решения
1) По данным мощности предприятий за год в 2019 году составляют
| Предприятия с годовой мощностью, тыс.т | Количество предприятий |
| До 500 | |
| 500 – 1000 | |
| 1000 – 2000 | |
| 2000 – 3000 | |
| Свыше 3000 |
Построить гистограмму и кумулянту. Рассчитать среднюю мощность предприятий. Найти дисперсию и коэффициент вариации. Проанализировать результаты.
2) Постройте гистограмму частот, найдите среднюю заработную плату работников одного из транспортных цехов
| Заработная плата, у.е | 50–70 | 70–100 | 100–150 | 150–175 | 175–200 | 200-225 |
| Число работников |
Найти среднее квадратическое отклонение, коэффициент вариации заработной платы.
3) Для оценки состояния деловой активности предприятий были проведены обследования и получены следующие результаты:
| Показатель деловой активности | 0 – 8 | 8 – 16 | 16 – 24 | 24 - 32 |
| Число предприятий |
Построить гистограмму распределения частот. Найти среднее значение показателя деловой активности, дисперсию, коэффициент вариации.
4) При обследовании 50 комплектов для ремонта транспортных средств установлено следующее количество запасных элементов в комплектах: 5; 4; 3; 1; 4; 5; 3; 8; 10; 1; 3; 2; 5; 6; 7; 3; 5; 2; 3; 6; 8; 3;3; 5; 5; 6; 5; 4; 8; 5; 6; 4; 8; 7; 4; 5; 7; 8; 6; 5; 7; 5; 7; 6; 7; 3; 5; 7; 3; 4. Составить вариационный ряд распределения частот. Построить кумулянту. Найти выборочное среднее и дисперсию.
5) Постройте гистограмму частот, найдите среднюю арифметическую, среднее квадратическое отклонение и коэффициент вариации для данных о выручке компании на длительной зарубежной техновыставке.
| Выручка, у.е. | 0-200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 |
| Число дней |
6) Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей (Х) и стоимостью ежемесячного тех. обслуживания (Y). Для выяснения характера этой связи было отобрано 15 автомобилей.
| Х | |||||||||||||||
| Y |
Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при α = 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.
1.5. Оценки и методы их нахождения: метод моментов и метод максимального правдоподобия
Одна из задач математической статистики - оценить неизвестные истинные параметры генеральной совокупности.
Любая числовая функция от выборки является статистикой.
Статистика называется оценкой параметра, если при любом значении выборки считают ее значение приближенно равным неизвестному параметру.Существует ряд свойств, предъявляемых к оценкам неизвестного числового параметра, при выполнении которых оценка считается разумной.
Пусть θ- неизвестный параметр изучаемой случайной величиныX.
Оценка 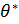 называется несмещенной, если ее математическое ожидание равно оцениваемому параметру
называется несмещенной, если ее математическое ожидание равно оцениваемому параметру 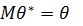 .
.
Оценка 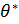 называется состоятельной, если она сходится по вероятностик оцениваемому параметру, т. е.
называется состоятельной, если она сходится по вероятностик оцениваемому параметру, т. е.
для всякого 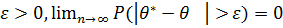 .
.
Поскольку функций от выборки можно придумать много, то нужно условиться о разумности применяемых оценок. Будем считать оценку разумной, если она несмещенная и состоятельная.
Существует несколько методов полученияоценок параметров случайных величин.
Метод моментовзаключается в приравнивании эмпирических (выборочных) моментов, вычисленных по данной выборке, и теоретических, вычисленных по предполагаемой плотности распределения, содержащей неизвестные параметры. Если число полученныхмоментов равно числу неизвестных параметров распределения,получают систему уравнений для вычисления этих неизвестныхпараметров.
Пример 1.
Найти методом моментов по выборке точечную оценку 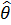 неизвестного параметра
неизвестного параметра 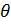 данного распределения случайной величины, заданной плотностью вероятностей
данного распределения случайной величины, заданной плотностью вероятностей 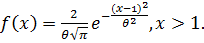
Рассмотрим математическое ожидания случайной величины, используя формулу вычисления математического ожидания для непрерывной случайной величины: 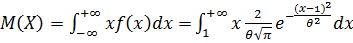 .
.
Вычислив данный интеграл, используя замену переменной, получаем:
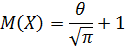
Найденное математическое ожидание (теоретический момент первого порядка) приравниваем соответствующему эмпирическому моменту (в нашем случае, выборочному среднему): 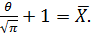
При решении уравнения относительно параметра 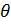 , получаем точечную оценку
, получаем точечную оценку 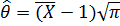 .
.
Ещё одним методом нахождения оценок является метод максимального правдоподобия, который состоит в нахождении значений неизвестного параметра распределения, при которомфункция правдоподобия достигает максимума, которую мы определим ниже.
Функцией правдоподобия случайной выборки 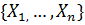 из генеральной совокупности X, закон распределения которой известен с точностью до параметра
из генеральной совокупности X, закон распределения которой известен с точностью до параметра 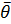 , называется функция, определяемая какпроизведение вероятностей
, называется функция, определяемая какпроизведение вероятностей 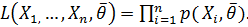 В случае если генеральная совокупность имеет непрерывное распределение с плотностью вероятности известной с точностью до параметра, функция правдоподобия имеет вид
В случае если генеральная совокупность имеет непрерывное распределение с плотностью вероятности известной с точностью до параметра, функция правдоподобия имеет вид 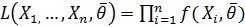 .
.
Оценка 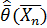 максимального правдоподобияпараметра
максимального правдоподобияпараметра 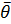 должна удовлетворять условию (необходимому условию экстремума):
должна удовлетворять условию (необходимому условию экстремума):
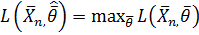 .
.
Для упрощения вычислений обычно используется логарифмирование, при котором точки экстремума остаются теми же, а уравнения упрощаются. Тогда условие записывается в следующем виде
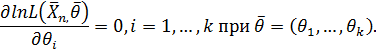
Полученные уравнения называются уравнениями правдоподобия.После того как получены их решения, можно дополнительно проверить достаточные условия максимума.
Пример 2.
Используя метод максимального правдоподобия найти точечную оценку 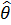 неизвестного параметра
неизвестного параметра 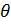 заданного распределения случайной величины, заданной следующей плотностью вероятностей:
заданного распределения случайной величины, заданной следующей плотностью вероятностей:
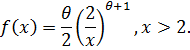
Составим функцию правдоподобия в случае непрерывного распределения:
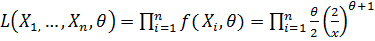 .
.
Удобно рассмотреть логарифмический вид функции правдоподобия. Тогда используя свойства логарифмирования, получим:
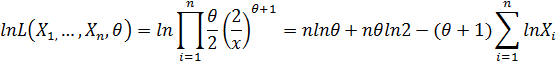
Далее решаем уравнение правдоподобия:
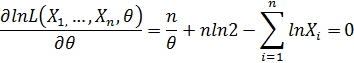
Данное уравнение решаем относительно 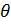 :
: 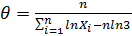 .
.
Задачи для самостоятельного решения
1) Найти методом моментов точечную оценку неизвестных параметра 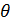 распределения случайнойвеличины, заданного плотностью вероятности:
распределения случайнойвеличины, заданного плотностью вероятности: 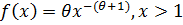 .
.
2) Найти методом моментов точечную оценку неизвестных параметров 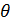 распределения случайнойвеличины, заданного плотностью вероятности:
распределения случайнойвеличины, заданного плотностью вероятности: 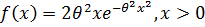 .
.
3) Найти методом максимального правдоподобия точечную оценку неизвестных параметров 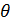 распределения случайнойвеличины, заданного плотностью вероятности:
распределения случайнойвеличины, заданного плотностью вероятности: 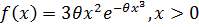 .
.
4) Найти методом максимального правдоподобия точечную оценку неизвестных параметров 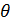 распределения случайнойвеличины, заданного плотностью вероятности:
распределения случайнойвеличины, заданного плотностью вероятности:  .
.
1.6.Интервальное оценивание
Доверительным интервалом для параметра θназывается интервал  , для которого выполняется
, для которого выполняется 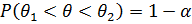 . Число 1−α называют доверительной вероятностью, азначение α — уровнем значимости.
. Число 1−α называют доверительной вероятностью, азначение α — уровнем значимости.
Точные доверительные интервалы строятся, как правило, в предположении нормальности данных. При том, что реальные данные могут не выглядеть нормальными, тем не менее широкое практическое применение описываемых методов дает достаточно неплохие результат (что объясняется, в частности, асимптотической нормальностью оценок).
Для оценки математического ожидания aнормально распределенной совокупности при известном среднем квадратическом отклоненииσпо выборке объемаnможно использовать следующую формулу
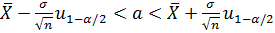 ,где
,где 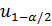 – квантиль уровня
– квантиль уровня 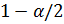 нормального распределения (определяется по таблицам).
нормального распределения (определяется по таблицам).
Для оценки математического ожидания анормально распределённой совокупности при неизвестной дисперсии 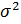 генеральной совокупности
генеральной совокупности
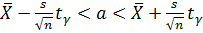 ,где
,где 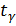 – критическая точка распределения Стьюдента (для двусторонней области) с n-1степенями свободы и уровнем значимости
– критическая точка распределения Стьюдента (для двусторонней области) с n-1степенями свободы и уровнем значимости 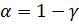 , s – исправленное выборочное среднее квадратическое отклонение; n- объём выборки.
, s – исправленное выборочное среднее квадратическое отклонение; n- объём выборки.
Для неизвестной дисперсии  ,где
,где 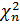 –критические точки
–критические точки 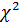 -распределения с n-1 степенями свободы и соответствующими уровнями значимости,
-распределения с n-1 степенями свободы и соответствующими уровнями значимости, 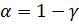 (определяется по таблицам).
(определяется по таблицам).
Пример 3.
Для компании, занимающейся поставками транспортных комплектующих, включающей 1200 офисов, составлена случайная выборка из 19 офисов. По выборке известно, что исправленное среднее квадратическое отклонение для числа работающих в офисе равно s=25 человек. Необходимо построить 90%-ный доверительный интервал для среднего квадратического отклонения числа работающих в офисе по всей компании.
Построим доверительный интервал дляпараметра 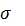 по формуле
по формуле  ,где
,где 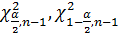 можно найти по таблице критических точек распределения хи-квадрат.Определяем по таблице
можно найти по таблице критических точек распределения хи-квадрат.Определяем по таблице 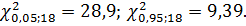 Далее подставляем в формулу найденные табличные значения и необходимые величины и получаем искомый доверительный интервал:
Далее подставляем в формулу найденные табличные значения и необходимые величины и получаем искомый доверительный интервал:
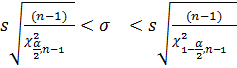 ,
, 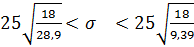
Получаем 19,74 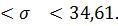
Задачи для самостоятельного решения
1) Для оценки готовности обработки новой партии комплектов по новой технологии были проанализированы 25 модификаций станков из нескольких подразделений предприятия. Получены следующие результаты в баллах: 107, 90, 114, 88, 117, 110, 103, 120, 96, 122, 93, 100, 121, 110, 135, 85, 120, 89, 100, 126, 90, 94, 99, 116, 111. По этим данным найдите 95%-й интервал для оценки среднего балла готовности обработки всех станков предприятия.
2) По данным 7 измерений некоторой величины найдены средняя результатов измерений, равная 32 и выборочная дисперсия, равная 38. Найти границы, в которых с надежностью 0,99 заключено истинное значение измеряемой величины.
3) Найти минимальный объём выборки, при котором с надежностью 0,95 точность оценки математического ожидания нормально распределенной случайной величины (по выборочному среднему) равна 0,2. Среднее квадратическое отклонение составляет 1,5.
1.7. Проверка статистических гипотез
Статистической гипотезой называется предположение о выборке, в частности, любое предположение о распределении генеральной совокупности.
Правило, по которому принимается решение, какая из гипотез больше всего соответствует выборочным данным, называется статистическим критерием (или критерием проверки гипотез).
Статистические гипотезы относительно истинного значения неизвестного параметра θ распределения некоторой случайной величины называют параметрическими гипотезами.
Выдвинутая гипотеза называется нулевой (или основной) гипотезойи обозначается 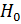 .Гипотеза, противоречащая нулевой, называетсяальтернативной (или конкурирующей), обозначается
.Гипотеза, противоречащая нулевой, называетсяальтернативной (или конкурирующей), обозначается 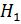 .
.
Цель статистической проверки гипотез состоит в том, чтобы на основании выборочных данных принять решение о справедливости основной гипотезы 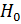 .
.
Гипотеза называется простой, если сводится к утверждению о том, что значение некоторого неизвестного параметра генеральной совокупности в точности равно заданной величине, в остальных случаях - сложной.
При проверке гипотезы возможно появление двух ошибок.
Ошибка 1-го рода заключается в том, что в доле случаев α нулевая гипотеза может оказаться отвергнутой, в то время как она справедлива. Вероятность этой ошибки называется уровнем значимости α.
Ошибка 2-го рода заключается в том, что в доле случаев β нулевая гипотеза принимается, в то время как на самом деле она ошибочна. Вероятность ошибки второго рода β. Вероятность 1-β называют мощностью критерия. Критерий называют более мощным, если из всех возможных критерием с заданным уровнем значимости α он обладает наибольшей мощностью.
Основным методом построения наиболее мощных статистических критериев является метод отношения правдоподобия.
Значение критерия, рассчитываемое по специальным правилам на основании выборочных данных, называется наблюдаемым значением критерия 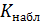 .Значения критерия, разделяющие совокупность значений критерия на область допустимых значений и критическую область, определяемые на заданном уровне значимости α по таблицам распределения случайной величины, выбранной в качестве критерия, называют критическими точками
.Значения критерия, разделяющие совокупность значений критерия на область допустимых значений и критическую область, определяемые на заданном уровне значимости α по таблицам распределения случайной величины, выбранной в качестве критерия, называют критическими точками 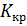 .
.
Областью допустимых значений называют совокупность значений критерия К, при которых нулевая гипотеза 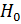 не отклоняется. Критической областью называют совокупность значений критерия К, при которых нулевая гипотеза
не отклоняется. Критической областью называют совокупность значений критерия К, при которых нулевая гипотеза 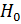 отклоняется в пользу конкурирующей
отклоняется в пользу конкурирующей 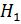 .Различают левостороннюю, правостороннюю и двусторонние критические области.
.Различают левостороннюю, правостороннюю и двусторонние критические области.
Основной принцип проверки статистических гипотез состоит в следующем:если наблюдаемое значение критерия принадлежит критической области, то нулевая гипотеза отклоняется в пользу конкурирующей,если наблюдаемое значение критерия принадлежит области допустимых значений, то нулевую гипотезу нельзя отклонить.
Пример 4.
Проверка гипотезы о неизвестном среднем 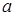 при неизвестной дисперсии
при неизвестной дисперсии 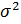 .
.
Основная гипотеза 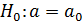 .Альтернативная гипотеза
.Альтернативная гипотеза 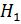 может быть трех видов:
может быть трех видов: 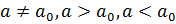 .
.
Для проверки используется статистика критерия 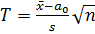
Для проверки берутся критические точки 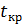 распределения Стьюдента с n-1 степенью свободы и уровнем значимости
распределения Стьюдента с n-1 степенью свободы и уровнем значимости 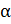 . Для случая
. Для случая 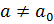 рассматривается двустороння критическая область, для остальных двух случае – односторонняя критическая область.
рассматривается двустороння критическая область, для остальных двух случае – односторонняя критическая область.
В случае 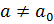 , если
, если  , то нулевая гипотеза принимается, если
, то нулевая гипотеза принимается, если 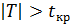 – отвергается.В случае
– отвергается.В случае 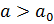 , если
, если 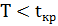 , то нулевая гипотеза принимается, если
, то нулевая гипотеза принимается, если 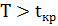 – отвергается.В случае
– отвергается.В случае 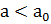 , если
, если 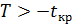 , то нулевая гипотеза принимается, если
, то нулевая гипотеза принимается, если 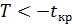 – отвергается.
– отвергается.
Пример 5.
Проверка гипотезы о неизвестном среднем 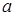 при известной дисперсии
при известной дисперсии 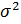 .
.
Основная гипотеза 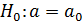 . Альтернативная гипотеза
. Альтернативная гипотеза 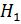 может быть трех видов:
может быть трех видов: 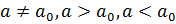 .
.
Для проверки используется статистика критерия 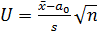 .
.
В случае 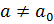 , критическая точка
, критическая точка 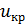 выбирается из условия
выбирается из условия 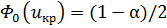 . Если
. Если 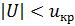 , то нулевая гипотеза принимается, если
, то нулевая гипотеза принимается, если 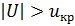 – отвергается.
– отвергается.
В остальных случая критическая точка 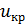 выбирается из условия
выбирается из условия 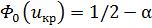 . В случае
. В случае 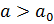 , если
, если 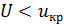 , то нулевая гипотеза принимается, если
, то нулевая гипотеза принимается, если 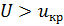 – отвергается.В случае
– отвергается.В случае 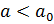 , если
, если 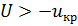 , то нулевая гипотеза принимается, если
, то нулевая гипотеза принимается, если 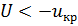 – отвергается.
– отвергается.
1.8 Критерии согласия
Критерии, относящиеся исключительно к виду функции распределенияили плотности распределения исследуемой случайной величины, называюткритериями согласия.
Следует понимать, что проверяют не то, что случайная величина действительно имеет определенный закон распределения, а лишь достаточно ли хорошо наблюдаемые данные согласуются с некоторым законом распределения, что помогает в дальнейшем использовать этот закон для прогнозирования поведения рассматриваемой случайной величины.
Одним из наиболее часто используемых критериев является критерий хи-квадрат Пирсона.
Пусть выдвинута гипотеза, что изучаемая случайная величина имеет функцию распределения 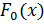 (или плотность распределения f(x)). Пусть далее вся область интервалов изменения величины Xразбита наrнепересекающихся полуинтервалов
(или плотность распределения f(x)). Пусть далее вся область интервалов изменения величины Xразбита наrнепересекающихся полуинтервалов 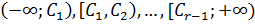 . Где
. Где 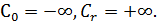 Пусть
Пусть 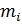 число выборочных значений, попавших в интервал
число выборочных значений, попавших в интервал 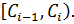
Алгоритм проверки гипотезы по критерию следующий.
1. Из генеральной совокупности производят выборку объема n.
2. По выборке составляют сгруппированный статистический ряд.
3. Весь диапазон значений разбивается на rчастичных интервалов.
4. На основании гипотетической функции распределения 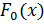 находят вероятности попадания случайной величины Х в частичные интервалы:
находят вероятности попадания случайной величины Х в частичные интервалы:
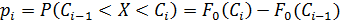 ,i=1,2,…,r.
,i=1,2,…,r.
5. Вычисляется статистика 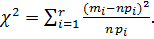 По теореме Пирсона получаем, что если
По теореме Пирсона получаем, что если 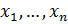 - выборка из генеральной совокупности с функцией распределения
- выборка из генеральной совокупности с функцией распределения 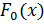 , то статистика
, то статистика 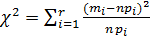 имеет при
имеет при 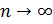 распределение хи-квадрат с r-1степенями свободы, если основная гипотеза верна.
распределение хи-квадрат с r-1степенями свободы, если основная гипотеза верна.
6. По таблице критических точек распределения хи-квадрат по заданному уровню значимости 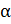 и числу степеней свободы r-1находятся критические точки
и числу степеней свободы r-1находятся критические точки 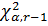 .
.
7. Проводится сравнение значение критерия с критическим значением:если 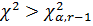 , то нулевая гипотеза отвергается в пользу альтернативной;если
, то нулевая гипотеза отвергается в пользу альтернативной;если 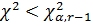 , то принимается нулевая гипотеза и считается, что гипотетическая функция распределения согласуется с опытными данными.
, то принимается нулевая гипотеза и считается, что гипотетическая функция распределения согласуется с опытными данными.
Если значения параметров гипотетической функции неизвестны, то рассматривается сложная гипотеза. При этом нулевая гипотеза заключается в том, что функция распределения имеет вид 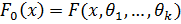 при некоторых неизвестных значениях параметров
при некоторых неизвестных значениях параметров 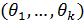 .
.
Критерий проверки в данном случае имеет вид:
 .
.
Так как истинные значения параметров 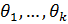 неизвестны, то подставляя их оценки, найденные методом максимального правдоподобия, критерий будет получен с меньшим числом степеней свободы r-k-1, где kчисло параметров гипотетической функции распределения.Гипотеза принимается, если
неизвестны, то подставляя их оценки, найденные методом максимального правдоподобия, критерий будет получен с меньшим числом степеней свободы r-k-1, где kчисло параметров гипотетической функции распределения.Гипотеза принимается, если 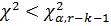 .
.
Гипотеза об однородности предполагает, что генеральные совокупности, из которых извлечены выборки, одинаковы и им соответствуют одинаковые функции распределения.
Часто рассматривают случай двух выборок k=2. Пусть есть два ряда наблюдений некоторого признака и каждый разбит на rгрупп. Сгруппированный ряд принимает вид:
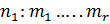 ,
, 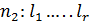 , где
, где 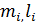 - число выборочных значений в i-й группе соответственно для первого и второго наблюдений. Статистический критерий для проверки нулевой гипотезы имеет вид
- число выборочных значений в i-й группе соответственно для первого и второго наблюдений. Статистический критерий для проверки нулевой гипотезы имеет вид 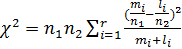 .
.
При 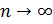 , если основная гипотеза верна, критерий имеет предельное распределение хи-квадрат с r-1степенями свободы. Проверка гипотезы проводится аналогично алгоритму проверки критерия, изложенному выше:если
, если основная гипотеза верна, критерий имеет предельное распределение хи-квадрат с r-1степенями свободы. Проверка гипотезы проводится аналогично алгоритму проверки критерия, изложенному выше:если 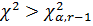 , то нулевая гипотеза отвергается в пользу альтернативной;если
, то нулевая гипотеза отвергается в пользу альтернативной;если 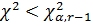 , то принимается нулевая гипотеза и считается что гипотетическая функция распределения согласуется с опытными данными.
, то принимается нулевая гипотеза и считается что гипотетическая функция распределения согласуется с опытными данными.
Задачи для самостоятельного решения
1) Экономический анализ производительности труда предприятий позволил выдвинуть гипотезу о наличии 2 типов предприятий с различной средней величиной показателя производительности труда. Выборочное обследование 42 предприятий 1-й группы дало следующие результаты: средняя производительность труда 119 деталей. Выборочное обследование 35 предприятий 2-й группы показало, что средняя производительность труда составляет 107 деталей. Генеральные дисперсии соответственно равны 127,91 и 135,1. Считая, что выборки извлечены из нормально распределённых генеральных совокупностей Х и Y,на уровне значимости 0.05, проверьте, случайно ли полученное различие средних показателей производительности труда или же имеются 2 типа предприятий с различной средней величиной производительности труда.
2) Партия изделий принимается в том случае, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0,98. Среди случайно отобранных 210 изделий проверяемой партии оказалось 195 соответствующих стандарту. Можно ли на уровне значимости α = 0,02 принять партию.
3) Инженер по контролю качества проверяет среднее время горения нового вида электроламп. Для проверки в порядке случайной выборки было отобрано 100 ламп, среднее время горения которых составило 1098 часов. Среднее квадратическое отклонение времени горения составляет 112 часов. Используя уровень значимости α = 0.05, проверьте гипотезу о том, что среднее время горения ламп – более 1000 часов.
4) По результатам n = 7 независимых измерений найдено, что 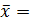 82,48 мм., а S=0,08 мм. Допустив, что ошибки измерения имеют нормальное распределение проверить на уровне значимости α=0,05 гипотезу
82,48 мм., а S=0,08 мм. Допустив, что ошибки измерения имеют нормальное распределение проверить на уровне значимости α=0,05 гипотезу 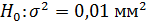 . против конкурирующей гипотезы
. против конкурирующей гипотезы 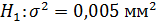 .
.
5) Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X по результатам выборки:
| X | 0,3 | 0,5 | 0,7 | 0,9 | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 |
| N |
6) Отдел технического контроля проверил n партий однотипных изделий и установил, что число X нестандартных изделий в одной партии имеет эмпирическое распределение, приведенное в таблице, в одной строке которой указано количество xi нестандартных изделий в одной партии, а в другой строке – количество ni партий, содержащих xi нестандартных изделий. Требуется при уровне значимости α=0,05 проверить гипотезу о том, что случайная величина X (число нестандартных изделий в одной партии) распределена по закону Пуассона.
| xi | ||||||
| ni |
7) При контроле изделий в цехе были измерены диаметры 300 валиков из партии, изготовленной одним станком. В таблице приведены отклонения измеренных диаметров от номинала. На уровне значимости 0,05 проверить гипотезу, что отклонение диаметров от эталона можно описать нормальным распределением.
| Границы отклонений | Середина интервала | Число валиков | Границы отклонений | Середина интервала | Число валиков |
| -30…-25 | -27,5 | 0…5 | 2,5 | ||
| -25…-20 | -22,5 | 5…10 | 7,5 | ||
| -20…-15 | -17,5 | 10…15 | 12,5 | ||
| -15…-10 | -12,5 | 15…20 | 17,5 | ||
| -10…-5 | -7,5 | 20…25 | 22,5 | ||
| -5…0 | -2,5 | 25…30 | 27,5 |
2. ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
2.1. Введение. Систематические и случайные погрешности
В настоящей главе пойдет речь о статистических методах обработки экспериментальных данных. Под экспериментальными данными мы будем понимать некоторую выборку, каждым элементом которой является пара значений «фактор»-«зависимая переменная». Фактор – это значение независимой переменной, характеризующей условия эксперимента, параметры, при которых производятся измерения. Значением фактора может быть одно число, числовой вектор. Зависимая переменная – значение измеряемой в эксперименте величины. Это также может быть число либо числовой вектор. Далее мы будем рассматривать только зависимые переменные, описываемые одним числом. В качестве примера рассмотрим эксперимент по измерению величины прогиба балки при различных значениях механической нагрузки и температуры. Факторами в данном эксперименте являются две величины: механическая нагрузка и температура. Зависимой переменной – измеряемый в эксперименте прогиб балки, характеризуемый одним числом.
В любом реальном эксперименте на значение зависимой переменной влияет не только значение учитываемых факторов, но и значение неучитываемых факторов: неточное знание условий эксперимента, влияние случайных воздействий внешней среды, несовершенство измерительных приборов и т.д. Влияние неучитываемых факторов вносит погрешность в результат эксперимента, которую можно разделить на две составляющих: систематическую погрешность и случайную погрешность. Случайная погрешность меняется от эксперимента к эксперименту при сохранении неизменными условий эксперимента. Математическое ожидание такой погрешности равно нулю и, таким образом, ее можно устранить или уменьшить, проведя большое количество однотипных измерений и усреднив по результатам этих измерений. В большинстве случаев распределение величины случайной погрешности можно считать нормальным с нулевым математическим ожиданием. Напротив, систематическую погрешность нельзя устранить усреднением по однотипным измерениям. Систематическая ошибка может быть вызвана тем, что в эксперименте не учтён какой-либо существенный фактор, который остается неизменным в данной серии измерений, но может иметь другое постоянное значение в другой серии. Другой возможный источник систематической погрешности – использование определенного измерительного прибора или методики измерений. Однако далее, если не оговорено иное, мы будем считать, что систематические погрешности отсутствуют.
Наконец, важно заметить, что выделение в эксперименте независимой переменной – фактора – и зависимой переменной зачастую носит условный характер. Математические методы позволяют лишь выявить закономерные связи между значениями условно выбранных факторов и зависимых величин, но не обосновать причинно-следственную связь между ними. Например, статистическое исследование какого-нибудь сообщества людей могло бы выявить закономерность, что люди с более темны
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|