Метод Симпсона

3. Метод Симпсона

В этом методе подынтегральная функция на частичном отрезке 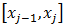аппроксимируется параболой, проходящей через три точки 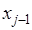, , 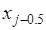, 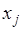то есть интерполяционным многочленом Лагранжа второй степени:

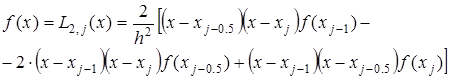
Проведя интегрирование, получим:

Это и есть формула Симпсона или формула парабол. На отрезке 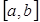формула Симпсона примет вид:

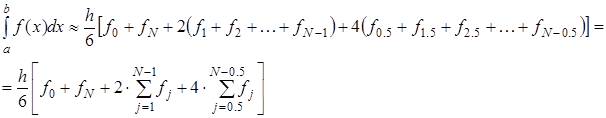
Если разбить отрезок интегрирования 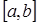на четное количество 2N равных частей с шагом 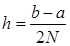, то можно построить параболу на каждом сдвоенном частичном отрезке 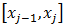и переписать выражения без дробных индексов. Тогда формула Симпсона примет вид:

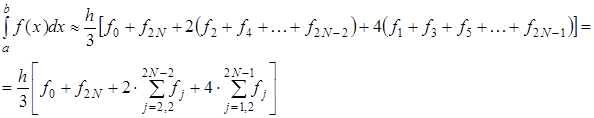(2.15)

Графическое представление метода Симпсона показано на рис.3. На каждом из сдвоенных частичных отрезков заменяем дугу данной кривой параболой.

⇐ Предыдущая 12