
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод трапеций
Методы Ньютона-Котеса
1. Метод прямоугольников
Одним из простейших методов численного интегрирования является метод прямоугольников. На частичном отрезке 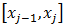 подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка 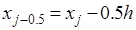 . Тогда значение интеграла на частичном отрезке: . Тогда значение интеграла на частичном отрезке:
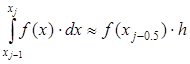 Подставив это выражение в формулу, получим составную формулу средних прямоугольников:
Подставив это выражение в формулу, получим составную формулу средних прямоугольников:
 Графическая иллюстрация метода средних прямоугольников представлена на рис.1(a). Из рисунка видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы N элементарных прямоугольников.
Формулу можно представить в ином виде:
Графическая иллюстрация метода средних прямоугольников представлена на рис.1(a). Из рисунка видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы N элементарных прямоугольников.
Формулу можно представить в ином виде:
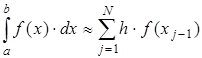 или или 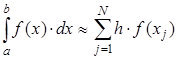 Эти формулы называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис.1(б, в). Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе средних прямоугольников.
Эти формулы называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис.1(б, в). Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе средних прямоугольников.
| ||||||
2. Метод трапеций
Если на частичном отрезке 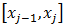 подынтегральную функцию заменить полиномом Лагранжа первой степени:
подынтегральную функцию заменить полиномом Лагранжа первой степени:

то искомый интеграл на частичном отрезке запишется следующим образом:
 (2.10)
(2.10)
Тогда составная формула трапеций на всем отрезке интегрирования 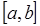 примет вид:
примет вид:

Графически метод трапеций представлен на рис.2. Площадь криволинейной трапеции заменяется площадью многоугольника, составленного из N трапеций, при этом кривая заменяется вписанной в нее ломаной. На каждом из частичных отрезков функция аппроксимируется прямой, проходящей через конечные значения, при этом площадь трапеции на каждом отрезке определяется по формуле 2.10.
Погрешность метода трапеций выше, чем у метода средних прямоугольников. Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда.

Рис.2. Интегрирование методом трапеций
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
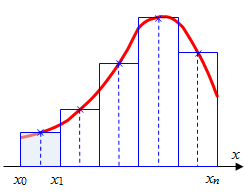 а) средние прямоугольники
а) средние прямоугольники
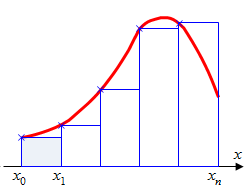 б) левые прямоугольники
б) левые прямоугольники
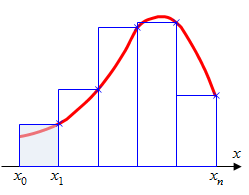 в) правые прямоугольники
в) правые прямоугольники