Решение.. Доказательство.

Решение.

Обозначим события:

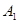– деталь изготовлена первым автоматом;

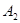– деталь изготовлена вторым автоматом;

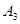– деталь изготовлена третьим автоматом.

Вероятности этих событий, по классической формуле (1.3):

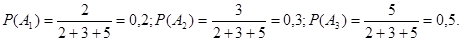
Эти события составляют полную группу попарно несовместных событий, так как никакие два из этих событий не могут произойти одновременно, и сумма их вероятностей равна 1.

Событие В – наудачу взятая деталь из общей продукции автоматов – стандартное и происходит одновременно с одним из событий 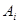. Условные вероятности события В согласно условию задачи:

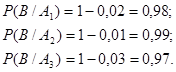
По формуле полной вероятности (1.22):

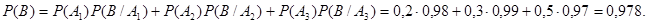
§ 3.2. Формула Байеса[1]

Если уже наступило рассматриваемое некоторое событие В, происходящее с одним из событий 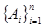образующих полную группу попарно несовместимых событий, причем известны вероятности этих гипотез до испытания 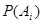, а также вероятности, сообщаемые ими событию В: 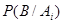, то можно рассчитать вероятности гипотез 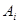– после того, как событие В произошло.

Формула Байеса

Вероятность 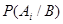гипотезы 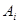, при условии, что событие В произошло:

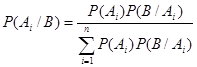. (1.23)

Доказательство.

По теореме умножения для зависимых событий (1.19):

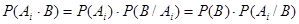из чего следует, что .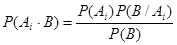

В соответствии с формулой полной вероятности (1.22):

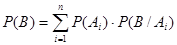следовательно

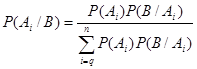Вероятности гипотез до испытания 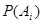называют еще априорными(доопытными), а вероятности гипотез 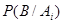, после того как произошло событие В, называют апостериорными(послеопытными).

Формула Байеса, таким образом, дает возможность «пересмотреть» вероятности гипотез с учетом наблюденного результата опыта, по мере получения новой информации. Это имеет большое научно-практическое значение.

Пример 3.2. Наборщик типографии использует 2 набора шрифтов одинакового объема, при этом в первом наборе 80%, а во втором – 70% отличного шрифта. Наудачу извлеченная литера оказалась отличного качества. Найти вероятность того, что эта литера взята из второго набора.

Решение.

Обозначим события:

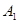–литера извлечена из первого набора;

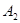– литера извлечена из второго набора.

Так как по условию наборы шрифтов имеют одинаковый объем, то вероятности этих событий:

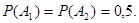
Эти события составляют полную группу попарно несовместимых событий, так как они не могут произойти одновременно, и сумма их вероятностей равна 1. Событие В – наудачу взятая литера отличного качества – происходит одновременно с одним из событий 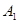. Условные вероятности события В согласно условию задачи:

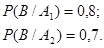
В задаче требуется переоценить вероятность события 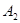при условии, что событие В произошло. По формуле Байеса (1.23):

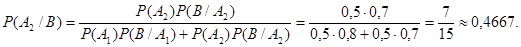
[1] Т. Байес(в некоторых источниках – Бейес) (Th. Bayes) – английский математик XVIII в.

⇐ Предыдущая 12