Тема 3. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ.

Тема 3. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ.

ФОРМУЛА БАЙЕСА

Следствием основных теорем теории вероятностей — теорем сложения и умножения вероятностей — является формула полной вероятности.

§ 3.1. Формула полной вероятности

Пусть рассматривается полная группа попарно несовместных co6ытий 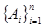, т. е. выполняются условия 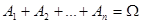, 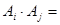Ø, 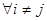, и некоторое событие В, которое может осуществиться одновременно только с одним из .

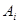Говорят еще, что об обстановке проведения опыта можно сделать n исключающих друг друга предположений 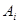, называемых гипотезами.

Формула полной вероятности.

Теорема.Вероятность Р(В) события В, которое может произойти только при условии появления одного из событий (гипотез) 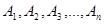, образующих полную группу попарно несовместных событий, равна сумме произведений вероятностей каждого из событий 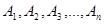на соответствующие условные вероятности события В:

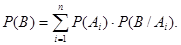(1.22)

Доказательство.

Рассмотрим произведение события 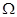на событие В:

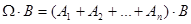Применяя свойства операций над событиями, получим:

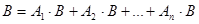События 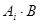и 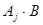несовместны 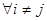, так как 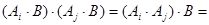Ø 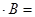Ø, поэтому в соответствии с теоремой сложения вероятностей для несовместных событий (1.13):

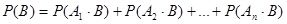Применяя далее теорему умножения для зависимых событий (1.19), получим:

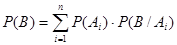Пример 3.1. На сборку поступают детали с трех станков-автоматов, производительности которых соотносятся, как 2:3:5. Брак в продукции этих автоматов составляет 2%, 1% и 3% соответственно. Найти вероятность того, что наудачу взятая деталь из общей продукции автоматов – стандартная.

12 Следующая ⇒