Тема занятия: «Призма. Прямая и наклонная призма. Правильная призма. Формулы площади поверхностей призмы».

Стр 1 из 2Следующая ⇒

Тема занятия: «Призма. Прямая и наклонная призма. Правильная призма. Формулы площади поверхностей призмы».

Повтори необходимые формулы:

1. Прямоугольный параллелепипед

Пусть a, b, с – стороны, d – диагональ параллелепипеда,

S_n – полная поверхность.

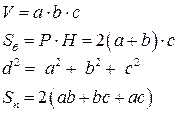
2.Куб

Пусть a – ребро куба.

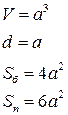
Опорные задачи.

1)Ребро куба равно a. Найдите: диагональ грани, диагональ куба, периметр основания, площадь грани, площадь диагонального сечения; площадь поверхности куба; периметр и площадь сечения, проходящего через концы трёх рёбер, выходящих из одной и той же вершины.

2)Площадь боковой поверхности правильной четырёхугольной призмы равна 32 см², а площадь полной поверхности 40 см². Найдите высоту призмы.

3)Расстояния между боковыми рёбрами наклонной треугольной призмы равны 2 см, 3 см и 4 см. Боковая поверхность призмы 45 см². Найдите боковое ребро.

4)В правильной n – угольной призме проведена плоскость под углом 60⁰ к основанию так, что она пересекает все боковые грани призмы. Площадь основания равна 50 см². Найдите площадь сечения.

Решение: S_осн=S_сеч*cos 60⁰

S_сеч=100см²

5)Существует ли призма, имеющая 50 рёбер? 54 ребра?

Решение: Число ребер n – угольной призмы 3n, поэтому призмы, имеющей 50 ребер, не существует, а 54 ребра имеет 18-угольная призма.

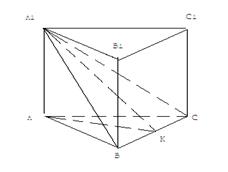
6)В правильной треугольной призме плоскость сечения BCА₁ образует с плоскостью основания двугранный угол φ. Постройте линейный угол этого двугранного угла. Дайте объяснение.

Построение: Проведём из вершины A правильного треугольника ABC высоту AK. Точка K принадлежит ребру BC. Соответственно, отрезок А₁К перпендикулярен ребру BC (по теореме о трёх перпендикулярах). Угол A₁КА– искомый.

12 Следующая ⇒