Хелпикс

Главная

Контакты

Случайная статья



Пример №4. Вычислить.

⇐ ПредыдущаяСтр 3 из 3


Пример №4

Упростить выражение: cos(α + β) + cos(α - β)

Решение: воспользовавшись формулами косинуса суммы косинуса разности, получим: cos(α + β) + cos(α - β) = cosαcosβ – sinαsinβ + cosαcosβ + sinαsinβ  = 2 cosαcosβ

 

3.Домашнее задание:

 

1.Посмотреть ОБЯЗАТЕЛЬНО видеоуроки :   https://youtu.be/-Uxf_V6FIuE

 https://youtu.be/HmQliRR1V5k      https://youtu.be/bK7zcql6SXs

2. Прочитать учебник стр.142- 146 . п.27 .п.28, разобрать примеры из данного параграфа. , сделать опорный конспект(выписать все формулы- и выучить их!!!)

3.Выполнить упр.№ 475(1,2,3,4) , 476 (1,2,3) ,481(2,4).482( 1,3,4)484(1,2), 485( 1,2)

.Самостоятельная работа по изученной теме9все задания решать ,а не ответы только писать):

1.Вычислить.

соs(-π)+ctg(-π/2)-sin(-3π/2)+ctg(-π/4)=

2.Упростите:

a) sin 150cos450 – cos150 sin450

б) sinα cos3α -  cosα sin3α

в) sin 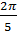 cos  -   sin со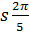

г) sin(α – 300)+ cos(600 + α)

д*) sin(2х+3у) cos(х -3у) +  sin(3у – х) cos(2х + 3у)

3*. Найдите sin(α – β) и cos(α + β), если sinα = 0,8 и

 сosβ = - 0,6  0,5π≤ α ≤π , 0,5π≤ β ≤π

Критерии оценивания:

Все задания решены без ошибок- оценка 5

Решены 1 и 2(кроме д) )-----оценка 4

Есть 2 ошибки в заданиях на оценку 4 –это оценка 3

 

 


⇐ Предыдущая123
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.