Контакты

Случайная статья

Синус суммы и разности аргументов

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Синус суммы и разности аргументов

Предварительно докажем формулы:

1) 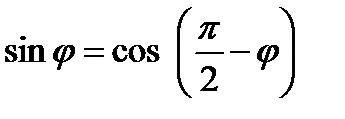; 2) .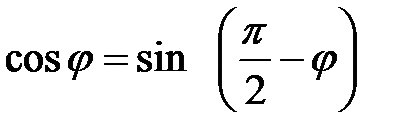

1) .

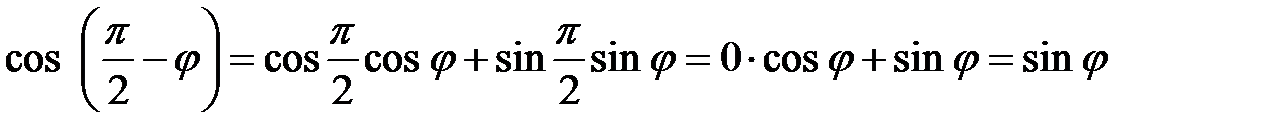2)

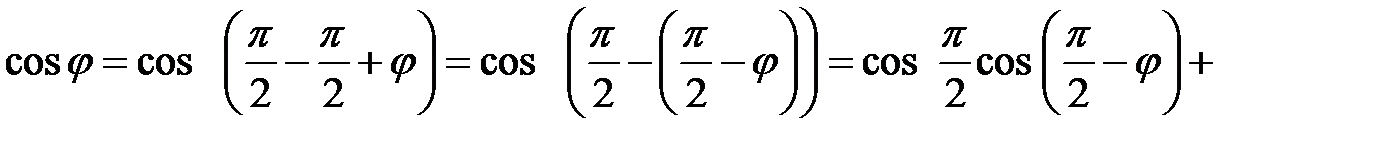
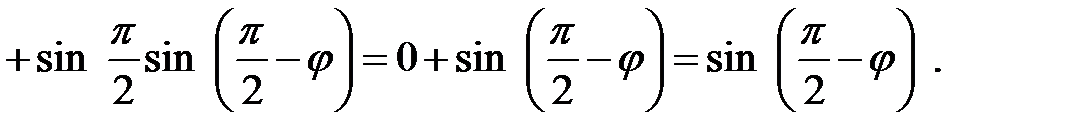
Теорема 1. Для любых углов 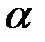и 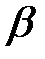справедливо тождество

.

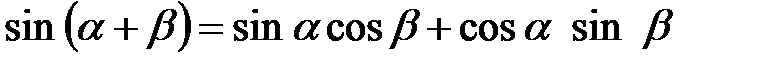Доказательство. Используя формулы 1) и 2), докажем теорему 1

■

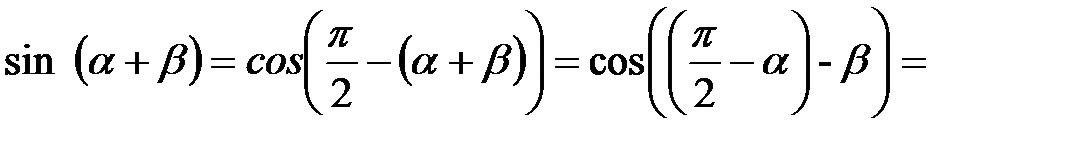
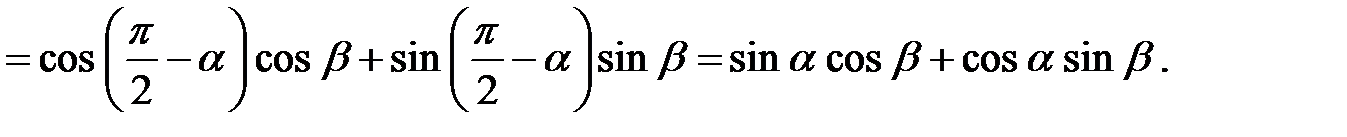Теорема 2. Для любых углов 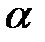и справедлива формула

.

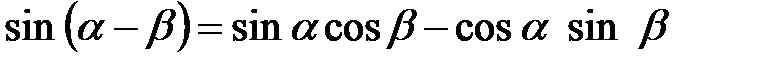Доказательство.

так как , .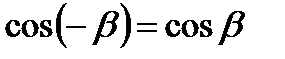

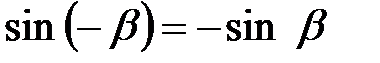Тангенс суммы и разности двух аргументов

Тангенс суммы двух аргументов можно получить из рассмотренных выше формул:

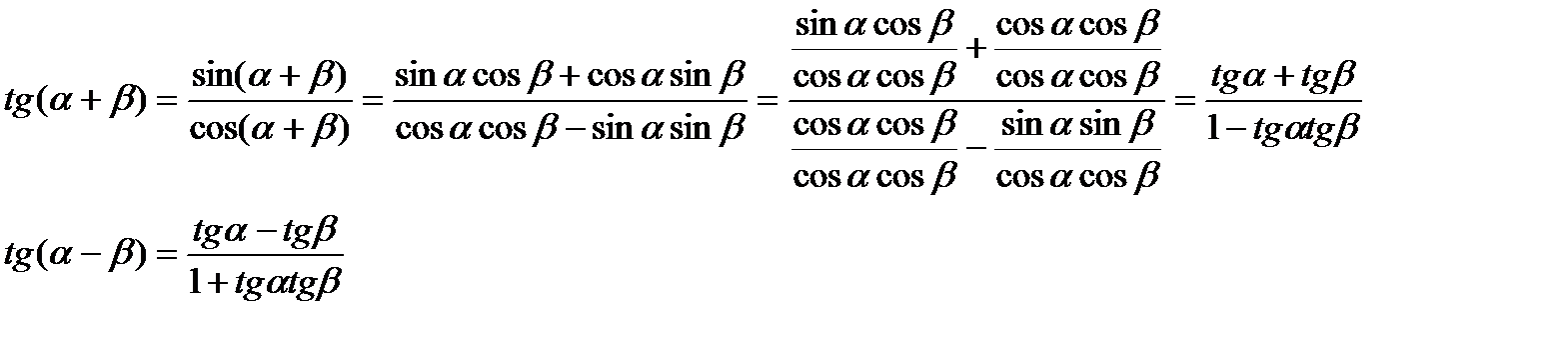
4. Упражнения для закрепления

Пример№1.

Используя формулы сложения, вычислить cos75⁰ ; sin75⁰.
Решение:

соs 75⁰ = cos(45⁰ + 30⁰) = cos45⁰cos30⁰ – sin45⁰sin30⁰ =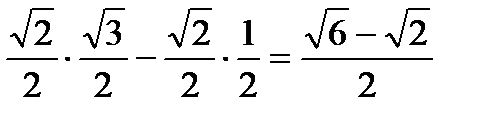

Sin 75⁰ = sin(45⁰ + 30⁰)= sin45⁰cos30⁰ + cos45⁰sin30⁰=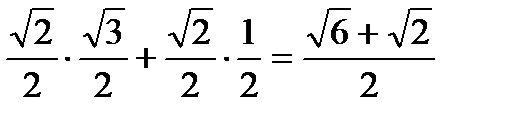

Закончите вычисления с помощью вышерассмотренных формул:

а) сos105⁰= cos(60⁰ +45⁰) =

б)sin15⁰ = sin(45⁰– 30⁰) = Пример №2.

Дано sinα = 0,6, sinβ = 0,8, π/2<α<π, π/2<β<π. Найти sin(α+β)

Решение: sin(α+β) = sinαcosβ+sinβcosα

Так как по условию задачи углы α и β принадлежат второй четверти, то cosα и cosβ имеют знак «минус». Используем формулs cos²α = 1-sin²α;

cos²β = 1-sin²β

cos²α = 1-0,6²= 1-0,36 = 0,64

cosα = - 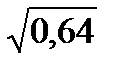= -0,8

cos²β = 1-0,8²= 1-0,64 = 0,36

cosα = - 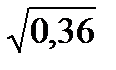= -0,6

Подставим полученные данные и имеющиеся в условии данные в формулу sin(α+β) = sinαcosβ+sinβcosα и выполним действия

sin(α+β) = 0,6·(-0,8)+0,8·(-0,6) = -0,48-0,48=-0,96

Используя решение примера №2 в качестве образца, вычислите cos(α + β), если sinα = 0,6, sinβ = 0,8, π/2<α<π, π/2<β<π

Пример №3.

Найдите значение выражения cos76⁰cos16⁰ + sin76⁰sin16⁰

Решение: cos76⁰cos16⁰ + sin76⁰sin16⁰ здесь развернутая формула косинуса разности двух углов. Вспомним, что 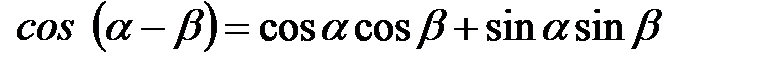, значит: cos76⁰cos16⁰ + sin76⁰sin16⁰ = cos(76⁰ – 16⁰) = cos60⁰ = 0,5

Вычислите самостоятельно:

а)sin58⁰cos13⁰ + cos58⁰sin13⁰

б)cos16⁰cos14⁰ – sin16⁰sin14⁰

⇐ Предыдущая 123 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.