Решить задачу № 264( решение оформляем в тетрадях!!!!!)

Решить задачу № 264( решение оформляем в тетрадях!!!!!)

Найдите площадь боковой поверхности правильной шестиугольной пирамиды, если сторона её основания равна а, а площадь боковой грани равна площади сечения, проведенного через вершину пирамиды и большую диагональ основания

S_бок = ½ P_осн. • d, S_бок = ½ • 6а• d. d - ?

10.

11.

12.

13.

А₁А₄ – большая диагональ правильного шестиугольника, поэтому А₁А₄=2R. R = А₁А₂ =a, то А₁А₄ = 2а.

*S_A1SA4 = ½ А₁А₄ • SO ; S_A1SA4 =½ • 2a•h. По усл.

S_A1SA4 = S_A3SA4. S_A3SA4 = ½ A₃ A₄ •SK, SK = 2h.

Р. SOK , О = 90⁰; SK=2 h, SO= h. OK= r, r = R cos (180⁰/n)

r= a•cos 30⁰ = 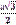. По теореме Пифагора находим:

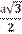( )²+ h²= 4h^{2 ;}h=а/2

SK = 2h = 2• = а.

S_бок = ½ • 6а• а = 3а².

Ответ: 3а²

Задача 1 ( в тетрадях)

Стороны основания правильной четырехугольной пирамиды равны 72, боковые ребра равны 164. Найдите площадь поверхности этой пирамиды.

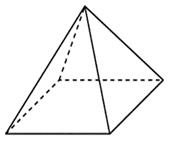
Площадь поверхности пирамиды равна сумме площадей боковой поверхности и основания:

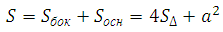
*Боковая поверхность состоит из четырёх равных по площади треугольников. Основание пирамиды это квадрат.

Площадь боковой стороны пирамиды можем вычислить воспользовавшись

Таким образом, площадь поверхности пирамиды равна:

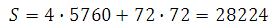
Ответ: 28224

Домашняя работа ( в течение дня!!!!!)

Задача 1.

Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды.

Задача 2

Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

2. Прочитать по учебнику п.28, 29 (ВЫУЧИТЬ ОСНОВНЫЕ ПОНЯТИЯ, ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ)

⇐ Предыдущая 12