Многогранники. Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.. Грани, пересекаясь, образуют ребра.. Упражнение

Стр 1 из 2Следующая ⇒

Многогранники

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.

Грани, пересекаясь, образуют ребра.

Ребра, пересекаясь, образуют вершины.

Рассмотрим два основных вида многогранников:

Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.

Упражнение

Дана пирамида, основание которой параллельно π₁. Основание представляет собой некоторый треугольник.

S – вершина пирамиды (Рисунок 6.1).

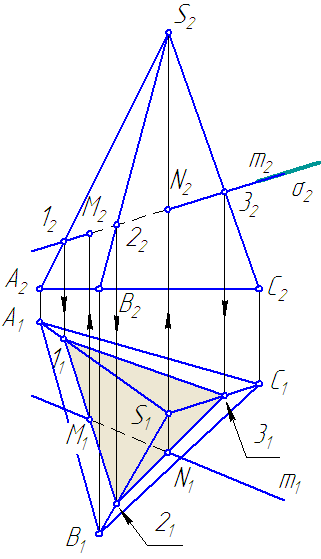
Рисунок 6.1 – Пересечение поверхности пирамиды прямой

Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.

Решение

Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.

Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).

Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции необходимо выполнять при помощи пропорционального деления отрезка.

В сечении находим точки M и N принадлежащие прямой m.
Определяем видимость прямойm.

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.

Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.

Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).

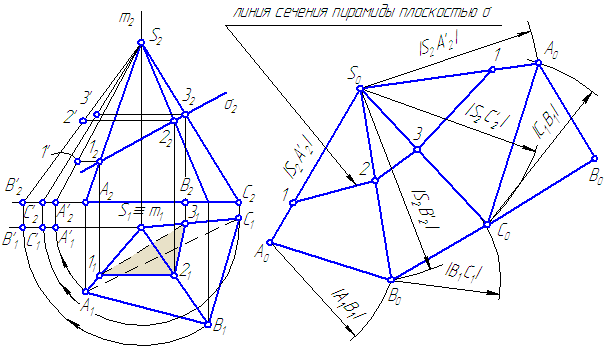
Рисунок 6.2 – Построение развёртки пирамиды

В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки 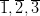, проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.

6.2. Призма. Развертка призмы

Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.

Упражнение

Дана призма, основания которой параллельны плоскости проекций π₁.

Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).

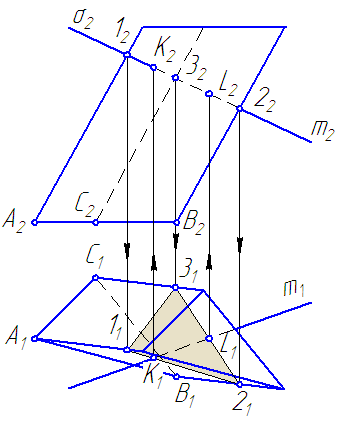
Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы

Порядок построения:

Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
В сечении находим точки K и L принадлежащие прямой m.
Определяем видимость прямойm. Если грань АВ на π₂ видна, то точкаК на π₂ видима, грань ВС невидима, следовательно, точка L невидима.

Рассмотрим наклонную призму. Пусть основание призмы параллельно π₁, а ребра параллельны π₂.

Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).

Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

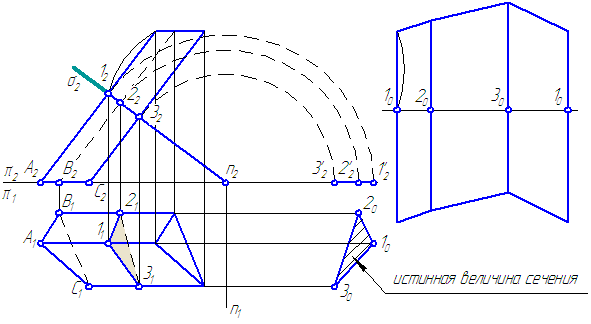
Рисунок 6.4 – Построение развёртки призмы

Порядок построения:

Найдем истинную величину сечения – (1₀2₀3₀), для чего повернём сечение (123) вокруг оси n⊥π₂, (можно ввести ДПП π₃//σ).
Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
/1₀-2₀/; /2₀-3₀/; /3₀-1₀/.

Проведём направления рёбер перпендикулярно этой линии через точки: 1₀; 2₀; 3₀ и отмерим вверх и вниз расстояния от нормального сечения (на π₂) до верхнего и нижнего основания, откладывая их на линиях-ребрах.

6.3. Взаимное пересечение многогранников

В результате пересечения многогранников получим ломаную линию.

Возможны два случая пересечения многогранников (Рисунок 6.5):

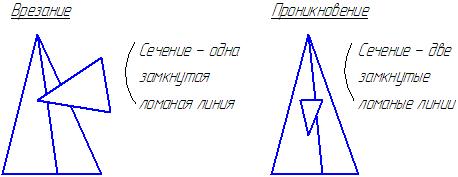
Рисунок 6.5 – Варианты пересечения многогранников

12 Следующая ⇒