Решение систем показательных и логарифмических уравнений

Решение систем показательных и логарифмических уравнений

На прошлом занятии мы вспомнили, как решаются системы уравнений. Мы продолжим решать системы уравнений, только уравнения будут показательными и логарифмическими. Эти системы решаются теми же способами, о которых мы говорили на прошлом занятии

Системы показательных уравнений

Решить системы уравнений:

Выразим у через х из (2) -го уравнения системы и подставим это значение в (1) -ое уравнение системы.

y=x+1

Решаем (2) -ое уравнение полученной системы:

2^х+2^x+2=10, применяем формулу: a^x+y=a^x∙a^y.

2^x+2^x∙2²=10, вынесем общий множитель 2^х за скобки:

2^х(1+2²)=10 или 2^х∙5=10, отсюда 2^х=2.

2^х=2¹, отсюда х=1. Возвращаемся к системе уравнений.

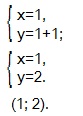
Ответ: (1; 2).

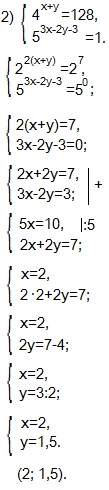
Представляем левую и правую части (1) -го уравнения в виде степеней с основанием 2, а правую часть (2) -го уравнения как нулевую степень числа 5

Если равны две степени с одинаковыми основаниями, то равны и показатели этих степеней — приравниваем показатели степеней с основаниями 2 и показатели степеней с основаниями 5.

Получившуюся систему линейных уравнений с двумя переменными решаем методом сложения.

Находим х=2 и это значение подставляем вместо х во второе уравнение системы.

Находим у.

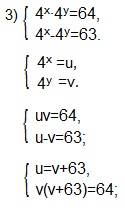
Решение.

Если в предыдущих двух примерах мы переходили к более простой системе приравнивая показатели двух степеней с одинаковыми основаниями, то в 3-ем примере эта операция невыполнима. Такие системы удобно решать вводом новых переменных. Мы введем переменные u и v, а затем выразим переменную u через v и получим уравнение относительно переменной v.

Решаем (2) -ое уравнение системы.

v (v+63)=64;

v²+63v-64=0. Подберем корни по теореме Виета, зная, что: v₁+v₂=-63; v₁∙v₂=-64.

Получаем: v₁=-64, v₂=1. Возвращаемся к системе, находим u.

Так как значения показательной функции всегда положительны, то уравнения 4^x=-1 и

4^y=-4 решений не имеют.

Представляем 64 и 1 в виде степеней с основанием 4.

Приравниваем показатели степеней и находим х и у.

12 Следующая ⇒