Тема:Предел функции непрерывного аргумента.

Тема:Предел функции непрерывного аргумента.

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. Записывается предел следующим образом .

Вычислим предел:
Подставляем вместо х число 3: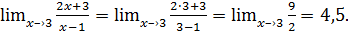
!Заметим, что предел числа равен самому числу.

Рассмотрим функцию у = f(x), где аргумент изменяется непрерывно (принимает значения из определенного промежутка, за исключением, возможно, одной внутренней точки данного промежутка).

Приведем два примера:

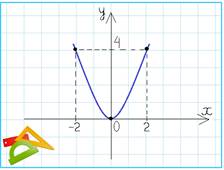
Пример 1: Проследим, как ведут себя значения функции f(x) = х2 + 2, если значение аргумента х как угодно близко приближаются к числу 2.

Обозначается х–˃2. Из рисунка следует, что если х–˃2 слева или справа, то соответствующие значения функции f(x) как угодно близко приближаются к числу 4, т.е. эти значения мало отличаются от числа 4.

В таком случае говорят, что функция f(x) = х²+ 2 имеет предел число 4 при х–˃2, или в точке х₀ = 2. Обозначается: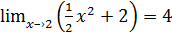

Пример 2: Проследим за значением функции при х–˃3.

В отличие от предыдущего примера, в точке х0 = 3 функция не определена. Однако по графику нетрудно сделать вывод, что если х–˃3 (х ≠ 3), то соответствующие значения функции приближаются к числу 6 - предел функции при х–˃3, или в точке х0 = 3, т.е. .

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).

Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.

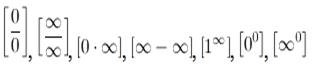
Основные виды неопределенностей:

12 3 Следующая ⇒