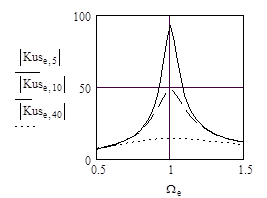Мост Вина-Робинсона.

Мост Вина-Робинсона.

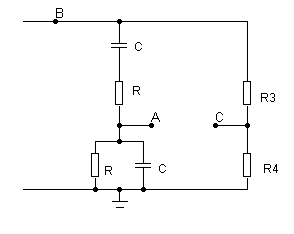Рис. 9. Принципиальная схема моста Вина-Робинсона.

Для увеличения избирательной способности моста Вина его применяют в сочетании с дополнительными цепями. Одним из примеров такого решения является параллельное соединение моста Вина с равными плечами (t1=t2) и резистивного делителя напряжения, которое называют мостом Вина-Робинсона. Принципиальная схема моста Вина-Робинсона представлена на рис. 9. В качестве входного напряжения примем напряжение Ub, а за выходное - напряжение Uac. Тогда коэффициент передачи по напряжению Kur моста Вина-Робинсона определяется как

Kur=Uac/Ub (25).

Выходное напряжение Uac моста Вина-Робинсона определяется как разность потенциалов двух точек:

Uac=Ua-Uc,

где каждую составляющую Ua и Uc можно найти через коэффициент передачи соответствующей ветви. Напряжения Ua является выходным напряжением моста Вина, а поэтому, используя (14), можно записать:

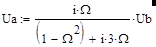(26),

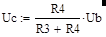Напряжение Uc является выходным напряжением резистивного делителя R3 – R4, а поэтому равно:

(27).

Тогда с учетом (26) и (27) коэффициент моста Вина-Робинсона будет равен:

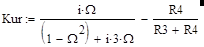(28).

Принято считать мост Вина-Робинсона уравновешанным, когда выходное напряжение Uac равно нулю. Так как коэффициент передачи моста Вина является частотозависимой функцией, то сбалансировать мост Вина-Робинсона можно только на одной частоте. Для равновесия моста на квазирезонансной частоте (Wо=1) моста Вина, когда его коэффициент передачи Kuo=1/3, коэффициент передачи резистивного делителя должен быть также равен 1/3. Для этого необходимо выбрать в резистивном делителе сопротивления, чтобы выполнялось соотношение:

R3=2*R4 (29).

Амплитудно-частотная характеристика ÷Kuro÷ =f(W) уравновешенного на квазирезонансной частоте моста Вина-Робинсона, построенная по (28), представлена на рис. 9., где для сравнения показана также амплитудно-частотная характеристика úKuVú=f(W) моста Вина.

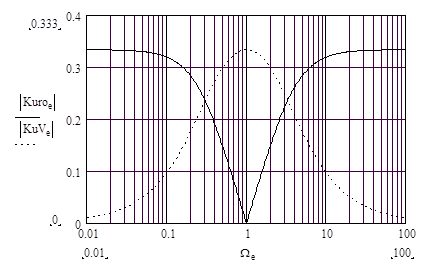
Рис. 9. Амплттудно-частотные характеристики уравновешенного на квазирезонансной частоте =1 моста Вина-Робинсона (Kuro) и моста Вина (KuV).

Амплитудно-частотная характеристика моста Вина-Робинсона соответствует частотной характеристики заградительного фильтра: на квазирезонансной частоте коэффициент передачи равен нулю, а при увеличении частотной расстройки устремляется к 1/3. Но такой фильтр далек от идеального, так как вне полосы заграждения имеет малый коэффициент пропускания

Основное применение мост Вина-Робинсона нашел в RC – генераторах, где используется в качестве частотозависимой цепи обратной связи. В таких генераторах напряжение с выхода усилителя (напомним, что любой генератор представляет собой усилитель, охваченный положительной обратной связи) подается на вход моста Вина-Робинсона, а выходное напряжение моста на вход усилителя. Поэтому в схеме генератора выходное напряжение моста Вина-Робинсона не может быть равным нулю, а отсюда уравновешенные мосты не используются. Разбаланс моста Вина-Робинсона достигают за счет небольшого отличия коэффициента передачи резистивного делителя от 1/3.

Рассмотрим характеристики неуравновешенного моста Вина-Робинсона, т.е. моста, у которого R3¹2*R4. Примем, что в мосте используется резистор R3 величиной:

R3=R3o*(1+e) (30),

где R3o – сопротивление, при котором мост Вина-Робинсона уравновешен, e – относительное отклонение сопротивления R3 от балансного R3o. В этом случаи коэффициент передачи резистивного делителя определится как:

Kud=R4/[R4+ R3o*(1+e)] (31).

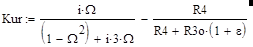Тогда вместо (28) для коэффициента передачи неуравновешенного моста Вина-Робинсона надо записать:

(32).

Отсюда следует, что на квазирезонансной частоте (Wо=1) коэффициент передачи неуравновешенного моста Вина-Робинсона равен:

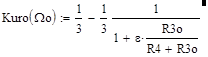(33).

Для небольших отклонение резистора R3 от R3o (e<1), проведя несложные преобразования, получим:

Kuro»(2/9)*e (34),

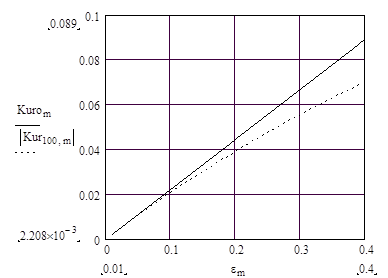
Рис. 10. Изменение коэффициента передачи моста Вина-Робинсона в зависимости от разбаланса e моста.

___ - по приближенной формулы (34), ….. – по формулы (33).

Зависимость коэффициента передачи неуравновешенного моста Вина-Робинсона от разбаланса e показывают, что выходное напряжение такого моста прямо пропорционально относительному отклонению резистора R3 от R3o. Приближенная формула (34) может быть использована в расчета при e< 0.1.

Амплитудно-частотные и фазо-частотные характеристики мост Вина-Робинсона находятся непосредственно из (33).

а) б)

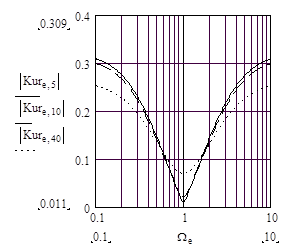
Рис. 11. Амплитудно-частотные (а) и фазо-частотные (б) характеристики моста Вина-Робинсона при различном разбалансе e.

___ - e = 0.05, - - - - e = 0.10, ….. - e = 0.40.

Сравнивая частотные характеристики моста Вина-Робинсона (рис. 11) и моста Вина (рис. 3), видим резкое отличие друг от друга. Во-первых, зависимости модулей коэффициентов передачи от частоты имеют противоположный характер: на квазирезонансной частоте он минимален у моста Вина-Робинсона и максимален у моста Вина. Во-вторых, фазо-частотные характеристики моста Вина-Робинсона имеют крутизну в диапазоне квазирезонансной частоты значительно больше, чем у моста Вина. Следует отметить, что уменьшение разбаланса e моста Вина-Робинсона приводит к возрастанию крутизны фазо-частотной характеристики.

При применении моста Вина-Робинсона в RC – генераторах одна из его ветвей, а именно мост Вина, используется в цепи положительной обратной связи усилителя. Вторая ветвь моста (резистивный делитель) образует в усилителе цепь отрицательной обратной связи. В стационарном режиме генерации выполняется баланс амплитуд, который сводится к тому, что:

koc * Kus = 1 (35),

где koc – коэффициент передачи цепи обратной связи, Kus – коэффициент усиления усилителя. Отсюда в стационарном режиме коэффициент усиления усилителя можно определить как:

Kus = 1 / koc (36).

Поэтому частотная характеристика обратной связи определяет частотную характеристику усилителя при условии, что собственный усилитель (без обратной связи) более широкополосен, чем цепь обратной связи. При использовании в генераторе несбалансированного (e¹1) моста Вина-Робинсона, т. е. когда koc=Kur, можно записать:

Kus = 1 / Kur (37),

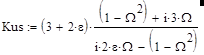где зависимость Kur от частоты сигнала определена (32). Проделав алгебраические преобразования, получим связь коэффициента усиления усилителя с частотой сигнала и разбалансом e моста:

(38).

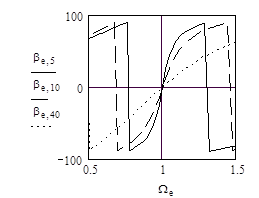
Соответствующие (38) амплитудно-частотные и фазо-частотные характеристики усилителя с мостом Вина-Робинсона показаны на рис. 12.

а) б)

Рис. 12. Амплитудно-частотные (а)) и фазо-частотные (б)) характеристики усилителя с неуравновешенным (e) мостом Вина-Робинсона в цепи обратной связи.

___ - e = 0.05, - - - - e = 0.10, ….. - e = 0.40.

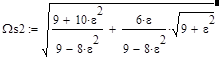Рассматривая частотные характеристики усилителя (рис. 12), отметим, что при использовании малого разбаланса моста они близки к аналогичным характеристикам резонансного контура высокой добротности. Как и для резонансных контуров, определим для усилителя с мостом Вина-Робинсона граничные частоты Ws1 и Ws2, в пределах которых коэффициент усиления уменьшается относительно величины на квазирезонансной частоте не более, чем 1/2¹^/² раза. Используя данное правило, из (38) найдем граничные частоты:

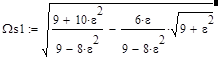(39).

Зная граничные частоты, оценим добротность квазирезонансного усилителя с мостом Вина-Робинсона как:

Qs=1/(Ws2-Ws1) (40).

Из (39) и (40) следует, что добротность квазирезонансного усилителя определяется только разбалансом e используемого моста Вина-Робинсона.

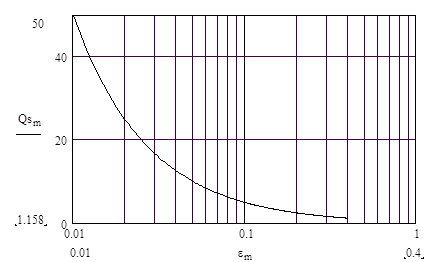
Рис. 13. Зависимость добротности квазирезонансного усилителя от разбаланса e моста Вина-Робинсона.

Представленная на рис.13 зависимость Qs от e показывает, что для получения добротности квазирезонансного усилителя более 20 мост Вина-Робинсона должен иметь e<0.03. Для такого малого разбаланса потребуется использовать в резистивном делителе моста высокоточные резисторы.

Таким образом, использование моста Вина-Робинсона в усилителе генератора гармонических сигналов позволяет резко сузить полосу усиления, что приводит к увеличению стабильности частоты генерации. Частота генерации, которая определяется квазирезонансной частотой моста Вина, несложно может манятся в широком диапазоне. Плавное изменение квазирезонансной частоты получают за счет использования спаренных переменных резисторов в мосте Вина, а дискретное – за счет переключения из набора конденсаторов. При этом изменение элементов моста Вина влияет только на величину квазирезонансной частоты и не меняет добротность усилителя. Поэтому относительная стабильность частоты генерации остается не зависимой от частоты генерации. Именно поэтому мост Вина-Робинсона нашел широкое применение в измерительных RC – генераторах, способных генерировать гармоническое напряжение в диапазоне от 10 Гц до 1 МГц.

⇐ Предыдущая 12