Мост Вина.

Мост Вина.

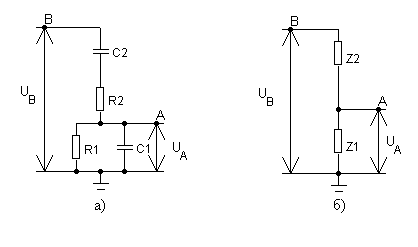
Рис.1. Принципиальная схема моста Вина.

Последовательно-параллельное соединение резисторов и конденсаторов, представленное на рис.1а, называют мостом Вина. Из-за наличия в мосте Вина конденсаторов его коэффициент передачи по напряжению, определяемый как отношение двух напряжений Ku=Ua/Ub, зависит от частоты f сигнала. Для анализа представим моста Вина в виде последовательного соединения двух комплексных сопротивлений Z1 и Z2, как показано на рис. 1б. Такую схему можно рассматривать как делитель напряжения из двух сопротивлений, коэффициент передачи Ku которого равен:

Ku=Z1/(Z1+Z2) (1)

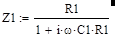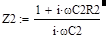Каждое комплексное сопротивление определяется параметрами элементов плеч и частотой w сигнала:

(2)

Первоначально определим величину Fu обратную коэффициента передачи Ku моста Вина:

Fu=1+Z2/Z1 (3)

Подставляя (2) в (3), находим:

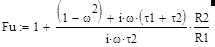(4 )

где t1=R1*C1и t2=R2*C2 – постоянные времени нижнего и верхнего плеч моста Вина. Из (4) следует, что Fu (соответственно и Ku) только на одной частоте wо=2*p*fo, когда (1-wо²)=0, является положительной действительной величиной, а на всех других частотах остается величиной комплексной. На данной частоте fo входное Ua и выходное Ub напряжения моста находятся в фазе, на всех других частотах между ними существует сдвиг по фазе. Данную частоту fo называют квазирезонансной частотой моста Вина, и она равна:

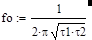(5),

Из (1) и (4) следует, что на квазирезонансной частоте коэффициент передачи Kuо моста Вина определяется параметрами своих элементов:

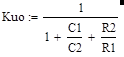(6).

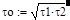Будем характеризовать квазирезонансную частоту wо моста Вина постоянной времени to=1/wо, которая связана с постоянными временами нижнего и верхнего плеча соотношением:

(7).

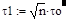Если при заданной квазирезонансной частоте wо выбрать постоянную времени нижнего плеча t1 равной:

(8),

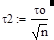где n – любое положительное число, то постоянная времени верхнего плеча t2 равна:

(9).

У такого моста с учетом (8) и (9) отношение емкостей конденсаторов связаны соотношением:

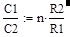(10),

а коэффициент передачи на квазирезонансной частоте Kuo равен:

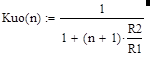(11).

На практике для плавной перестройки квазирезонансной частоты fo применяют в мосте Вина спаренные переменные резисторы и тогда R1=R2=R. В таком случаи коэффициент передачи Kuo моста Вина определяется только выбранным отношением постоянных времен нижнего и верхнего плеч n=t1/t2:

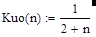(12).

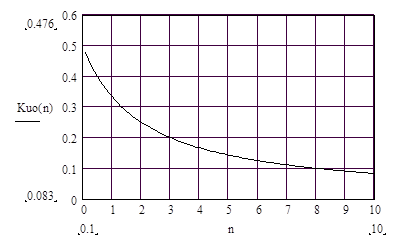
Рис. 2. Изменения коэффициента передачи Kuo моста Вина на квазирезонансной частоте в зависимости от отношения n постоянных времен нижнего и верхнего плеч (n=t1/t2).

Из (12) следует, что с уменьшением постоянной времени нижнего плеча t1 коэффициент передачи Kuo моста Вина устремляется к предельной величине, равной 0.5, а при уменьшении постоянной времени верхнего плеча t2 - к нулю. В частном случаи, когда постоянные времени равны t1=t2, коэффициент передачи Kuo=1/3.

Ниже рассмотрим характеристики моста Вина с равными резисторами R1=R2, наиболее часто используемого на практике. Проделав несложные преобразования, определим для такого моста из (4) зависимость коэффициента передачи от частоты сигнала, которая имеет следующий вид:

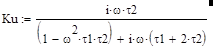(13)

Для получения результатов, независимых от выбора квазирезонансной частоты, введем нормированную частоту W сигнала, как W=w/wо. Подставляя (7) – (9) в (13), получим:

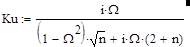(14).

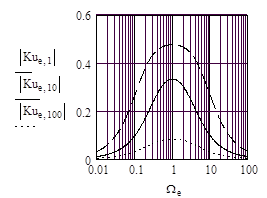
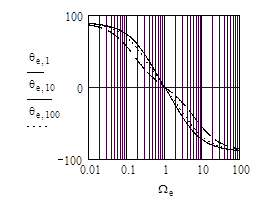
Из (14) можно получить амплитудно-частотные и фазо-частотные характеристики моста Вина, которые представлены на рис. 3.

а) б)

Рис. 3. Амплитудно-частотные (а) и фазо-частотные (б) характеристики моста Вина.

_ _ _ - отношение постоянных времен плеч n=0.1,

_____ - отношение постоянных времен плеч n=1,

…….. – отношение постоянных времен плеч n=10.

По виду частотные характеристики моста Вина подобны характеристикам избирательного LC – контура. Выбранное в мосте отношение постоянных времен плеч моста n определяет не только величина коэффициента передачи на квазирезонансной частоте Kuo(W=1) (рис. 2), но и полосу пропускания (рис. 3 а.), и крутизну фазо-частотных характеристик (рис. 3 б). Полосу пропускания моста определим как область нормированных частот W, в пределах которой модуль коэффициента передачи уменьшается не более, чем в 1/2^½ относительно Kuo. Для определения граничных частот W_1,2 полосы пропускания моста Вина воспользуемся (12) и (14), из которых имеем:

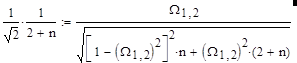(15).

Из решения уравнения (15) находятся граничные частоты:

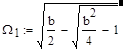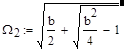(16),

где для сокращения записи использован параметр b, величина которого зависит только отношением n постоянных времен плеч:

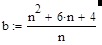(17).

Как квазирезонансную систему мост Вина охарактеризуем добротностью Q. В классическом понимании под добротностью резонансной системы понимают отношение запасенной в ней энергии к мощности потерь за период. При вычислении и измерении добротности резонансного контура используют соотношение, что она равна отношению резонансной частоты к полосе пропускания. Аналогично вычислим добротность Q моста Вина, когда используя нормированные частоты можно записать:

Q=1/(W₂-W₁) (18).

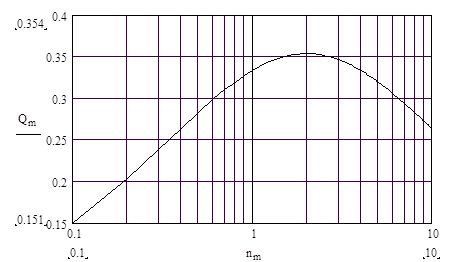Так как согласно (16) граничные частоты не зависят от номиналов R и С, а определяются только отношение n постоянных времен плеч, то и добротность моста Вина будет зависеть только от выбранного отношения n. Изменение добротности Q моста Вина от отношения n постоянных времен плеч показана на рис. 4.

Рис. 4. Изменение добротности Q моста Вина с R1=R2 в зависимости от отношения постоянных времени n=t1/t2 плеч.

Представленная на рис. 4 зависимости Q=f(n) показывает, что мост Вина с равными резисторами имеет максимальную добротность, когда С1=2*С2 (n=2). На практике в мосте используют конденсаторы постоянных номиналов, величины которых определяются стандартным дискретным рядом, а поэтому выполнить равенство С1=2*С2 сложно. Отсюда в основном используются мосты Вина с равными плечами (R=R1=R2 и C=С1=С2), так как при этом проигрыш в добротности оказывается небольшим. Однако отметим, что при любых выбранных параметрах моста Вина его добротность всегда остается меньше единицы, т.е. мост Вина является низкодобротной колебательной системой.

Выбор номиналов элементов (R и С) моста Вина проводят по заданной квазирезонансной частоте fo или, другими словами, заданной постоянной времени tо=1/2pfo. Но квазирезонансная частота определяется двумя параметрами, поэтому однозначно выбрать C и R по одному уравнению невозможно. Дополнительные требования к элементам моста возникают при анализе его работы в конкретном устройстве. Как правило, в устройстве задается входное напряжение моста, которое следует получить от генератора сигнала с известными характеристиками. В частности для такого генератора известно минимальное сопротивление нагрузки или величина тока, которая может быть от него отобрано. С другой стороны, подсоединение к выходу моста Вина устройства с входным импедансом Zвх, не должно изменять частотные характеристики моста. Первое дополнительное условие определяет требования к входному сопротивлению моста Вина. Независимость частотных характеристик моста обеспечивается, если элементы нижнего плеча удовлетворяют условию:

R1max<<Rвх С1мин>>Cвх (15),

Rвх и Свх – входные сопротивление и емкость устройства, подсоединяемого к выходу моста Вина.

Входное сопротивление Z3 моста Вина согласно рис. 1б определяется как:

Z3=Z1+Z2 (16).

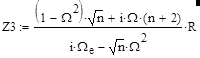Подставляя в (16) (2) и проделав алгебраические преобразования, получим для моста Вина с R=R1=R2 и C1=n*C2 зависимость входного сопротивления Z3 от нормированной частоты и отношения n постоянных времен плеч:

(17).

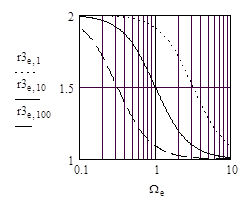
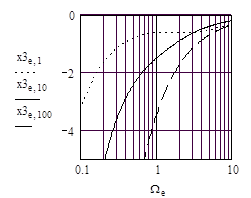
Из (17) следует, что входное сопротивление моста Вина на любой частоте сигнала, включая и квазирезонансную, имеет комплексный характер. Его можно представить в виде последовательного соединения действительного R3 и реактивного Х3 сопротивлений. Каждая составляющая зависит от частоты сигнала, а ход их изменений от частоты определяется выбранным отношением n постоянных времен плеч. Зависимости действительных R3 и реактивных Х3 компонент входного сопротивления от частоты сигнала показаны на рис. 6.

Рис. 6. Зависимости нормированных действительных r3=R3/R и реактивных x3=X3/R компонент входного сопротивления моста Вина от нормированной частоты W сигнала (R=R1=R2, C1=n*C2).

…… - для моста Вина с n=0.1,

____ - для моста Вина с n=1,

_ _ _ - для моста Вина с n=10.

Представленные на рис.6 зависимости компонент входного сопротивления показывают, что на любой частоте сигнала реактивная компонента входного сопротивления моста Вина имеет емкостной характер (х3<0). Соотношение между действительной и реактивной компонентами определяется выбранным отношением постоянных времен n=t1/t2 плеч. Для моста с n<1 реактивная компонента практически во всей области частот за исключением нижних (W<<1) меньше действительного сопротивления. Наоборот, для моста Вина с n>1 величина реактивной компоненты входного сопротивления, больше действительной. На квазирезонансной частоте Wo=1 согласно (17) входное сопротивление Z3o моста Вина с равными резисторами определяется как:

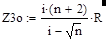(18)

Освобождаясь от мнимости в знаменателе, приведем его к виду:

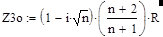(19).

Из (19) наглядно видно, что на квазирезонансной частоте действительная и реактивная компоненты входного сопротивления равны только у моста Вина с равными плечами (n =1). Для моста с n<1 больше действительное сопротивление, а при n>1 преобладает реактивная компонента. Модуль входного сопротивления |Z3o| на квазирезонансной частоте равен:

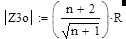(20).

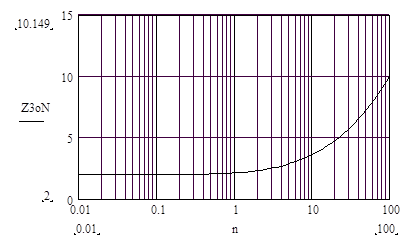Рис. 8. Зависимость нормированного модуля Z3oN=|Z3o|/R входного сопротивления моста Вина в зависимости от отношения постоянных времен плеч n=τ1/τ2.

Из (20) следует, что на квазирезонансной частоте модуль входного сопротивления моста Вина возрастает с увеличением n. Это соответствует тому, что при заданном входном напряжении Uб мосты Вина с n>1 отбирают от генератора меньший ток, чем мосты с n<1. В частном случаи, когда у равноплечного моста Вина (n=1), модуль входного сопротивления равен:

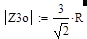(21).

На основе представленных выше характеристик моста Вина можно рекомендовать, что для получения квазирезонансной системы с максимальной добротностью следует применять мосты с равными плечами (t1=t2). В тех же случаях, когда необходимо иметь наибольшее входное сопротивление моста, то надо использовать мосты Вина с t1>>t2. Когда желательно для облегчения работы генератора сигнала уменьшить емкостную компоненту входного сопротивления моста, то следует в мосте Вина выполнить условие t1<<t2.

Учет зависимости входного сопротивления моста Вина от его элементов позволяет однозначно определить их номиналы. Например, если известен ток, который может быть отобран мостом при заданном напряжении Ub, то модуль входного сопротивления êZ3oêмоста Вина с t1=t2 должен быть не менее:

êZ3oê³ Ub/Id (22).

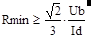Отсюда из (21) следует, что в мосте Вина можно использовать резисторы с минимальным сопротивлением Rmin:

(23).

Максимальное сопротивление Rmax резисторов ограничено условием (15). При выбранной величине резистора R по заданной квазирезонансной частоте fo следует определить из (5) величину емкости конденсатора:

С=1/2*p*fo*R (24).

Полученную емкость конденсатора С необходимо проверить на выполнение условия (15). Если величина конденсатора С моста Вина оказывается соизмеримой с входной емкостью Свх подсоединяемого устройства, то следует уменьшать сопротивление резистора R. Однако при этом потребуется увеличить отбираемый ток Id от генератора сигнала.

По рассчитанной по (24) емкости конденсатора С выбирается ближайший к ней номинал согласно стандартного ряда, а затем корректируется величина R. Резистор R, как указывалось выше, выбирается в виде переменного или подстроечного типа, пределы изменения которого позволяют получить необходимую величину.

12 Следующая ⇒