
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Понятие предела функции
Понятие предела функции
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала - самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
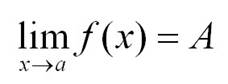
Lim - от английского limit - предел.
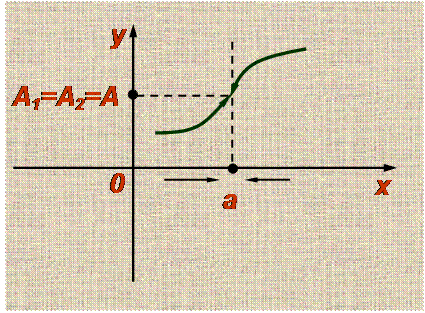
Существует также геометрическое объяснение определения предела. Посмотрите на рисунок, Видно, что , если х приближается к а, то значение функции приближается к A
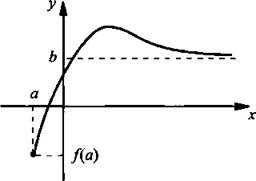
На этом рисунке видно, что, если х стремится к бесконечности, то значение функции приближается к b.
Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Рассмотрим теоремы, которые облегчают нахождение пределов функций.
 1. Предел суммы (разности) двух функций равен сумме (разности) пределов:
1. Предел суммы (разности) двух функций равен сумме (разности) пределов:
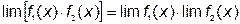 2. Предел произведения двух функций равен произведению пределов:
2. Предел произведения двух функций равен произведению пределов:
3. Постоянный множитель можно выносить за знак предела:
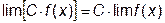 |
4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел
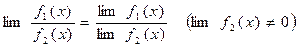 знаменателя не равен нулю:
знаменателя не равен нулю:
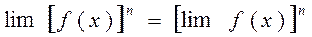 5. Предел степени с натуральным показателем равен той же степени предела:
5. Предел степени с натуральным показателем равен той же степени предела:
Приведем конкретный пример.
Задача - найти предел.
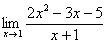
Любой предел состоит из трех частей:
1) Всем известного значка предела 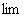 .
.
2) Записи под значком предела, в данном случае 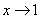 . Запись читается «икс стремится к единице». Чаще всего – именно
. Запись читается «икс стремится к единице». Чаще всего – именно 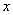 , хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность (
, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ( 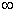 ).
).
3) Функции под знаком предела, в данном случае 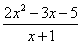 .
.
Сама запись 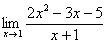 читается так: «предел функции
читается так: «предел функции 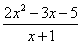 при икс стремящемся к единице».
при икс стремящемся к единице».
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала 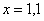 , затем
, затем 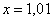 ,
, 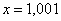 , …,
, …, 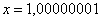 , ….
, ….
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
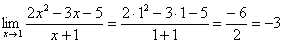
Готово.
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
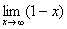
Разбираемся, что такое 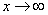 ? Это тот случай, когда
? Это тот случай, когда 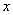 неограниченно возрастает, то есть: сначала
неограниченно возрастает, то есть: сначала 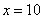 , потом
, потом 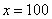 , потом
, потом 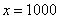 , затем
, затем 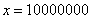 и так далее до бесконечности.
и так далее до бесконечности.
А что в это время происходит с функцией 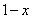 ?
?
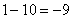 ,
, 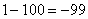 ,
, 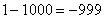 , …
, …
Итак: если 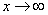 , то функция
, то функция 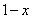 стремится к минус бесконечности:
стремится к минус бесконечности:
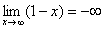
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию 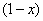 бесконечность и получаем ответ.
бесконечность и получаем ответ.
Еще один пример с бесконечностью:
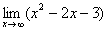
Опять начинаем увеличивать 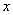 до бесконечности и смотрим на поведение функции:
до бесконечности и смотрим на поведение функции:
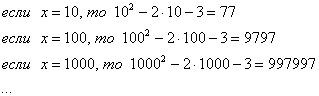
Вывод: при 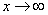 функция
функция 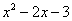 неограниченно возрастает:
неограниченно возрастает:
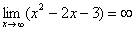
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|