Хелпикс

Главная

Контакты

Случайная статья



Механический смысл производной.

⇐ ПредыдущаяСтр 2 из 2


Механический смысл производной.

Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 + 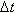точка перемещается на расстояние: x ( t0 + 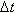) -x ( t0 ) = 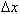, а её средняя скорость равна:va = 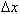/ 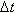. При 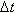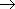0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0) материальной точки в момент времени t0 . Но по определению производной мы имеем:

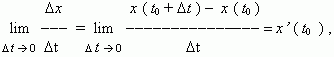
отсюда, v ( t0) =x’ ( t0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ).

Пример1.

Дан закон движения в точке x = etsin(t+ )

Найти скорость в точке t = 0.

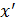 = etcos(t+ ) + etsin(t+ ) = e0cos(0+ ) + e0sin(0+ ) = 1+0 =1

Домашнее задание.

1.Вычислить производную в точке x0

y = sin5x, x0=0;

y= x6sin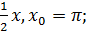

y = cos2x+x2/5 – 20, ;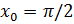

y = (3x – 2)5, x0=0;

2.Записать уравнение касательной к кривой в точке x0. Найти k, b.

1. y = 3x2 , x0=1;

2. y =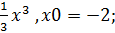

3.Найти скорость точки, движущейся по заданному закону, в моментto

1).S = tsin 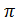t, to =1;2). S= 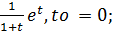3). S=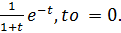


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.