Геометрический и физический смысл производной.

Стр 1 из 2Следующая ⇒

Геометрический и физический смысл производной.

Геометрический смысл производной.

Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке

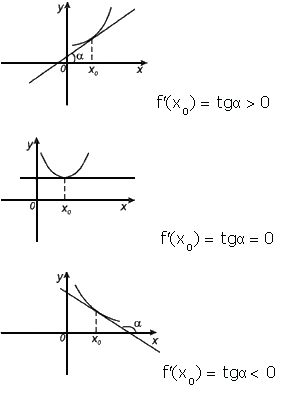
Уравнение касательной к графику функции y=f(x) в точке x₀ :

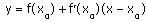
Физический смысл производной.

Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:

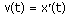
Примеры.

1. Найти значение производной функции

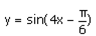
в точке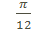

Решение.

Найдем производную данной функции по правилу дифференцирования сложной функции:

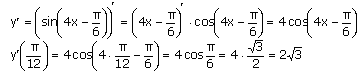Ответ: .

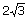2. Составить уравнение касательной к графику функции y=x+e^-2x, параллельной прямой y=-x

Решение.

Угловой коэффициент касательной равен значению производной в точке касания x₀. Т.к. касательная параллельна прямой y=-x, значит ее угловой коэффициент равен –1. Таким образом, f'(x₀)=-1. Найдем значение x₀.

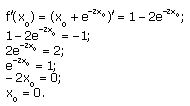
Уравнение касательной:

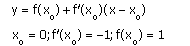
Уравнение касательной: y=1-1(x-0)=1-x

Ответ: y=1-x.

3. На параболе у=х²-2х-8 найти точку М, в которой касательная к ней параллельна прямой 4х+у+4=0.

Решение.

Определим угловой коэффициент касательной к параболе у=х²-2х-8:

k =у'=(х²-2х-8)'=2х-2.

Найдем угловой коэффициент прямой 4х+у+4=0:

у=-4х-4, k =-4.

Касательная к параболе и данная прямая по условию параллельны. Следовательно, их угловые коэффициенты равны, т.е.

2х-2=-4;

х=-1 – абсцисса точки касания.

Ординату точки касания М вычислим из уравнения данной параболы у=х²-2х-8, т.е.

у(-1)=(-1)²-2(-1)-8=-5, М(-1;-5).

Ответ: М(-1;-5).

12 Следующая ⇒