Контакты

Случайная статья

ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЙ.

⇐ ПредыдущаяСтр 2 из 2

2. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЙ.

Вычислить пределы функций.

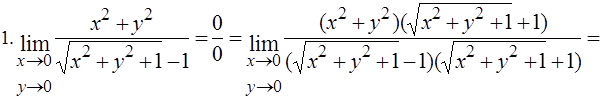
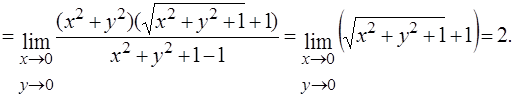
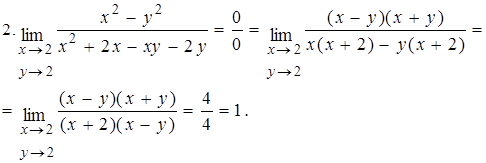
3.

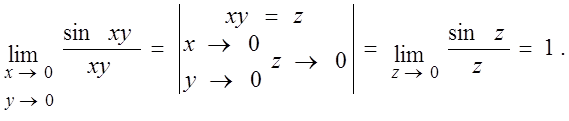
4.

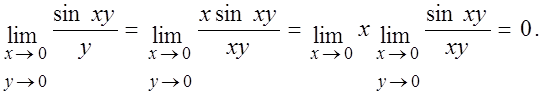
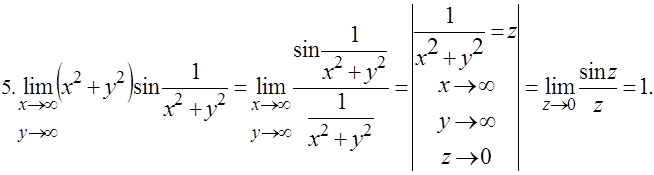
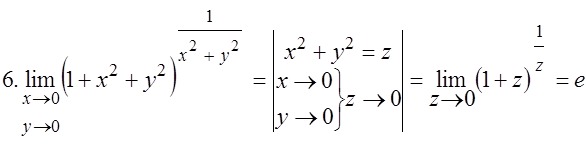
Найти точки разрыва функций:

7. .

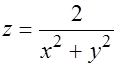Р е ш е н и е.

Найдём область определения функции.

x² + y² ¹ 0; область определения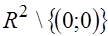

.

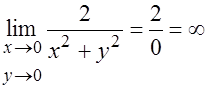Точка (0, 0) является точкой разрыва, вблизи этой точки функция может принимать сколь угодно большие положительные значения.

8. .

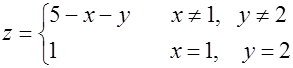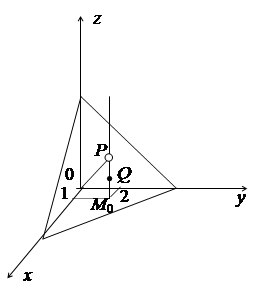
Данная функция разрывна в т. М₀(х₀, у₀), т. к. она определена вблизи этой точки и в самой точке, но её предел при 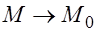не совпадает со значением функции в т.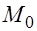

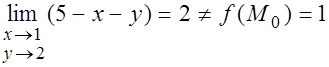
Графиком этой функции является плоскость 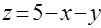без т. Р(1,2,2) вместо которой графику принадлежит т. Q(1,2,1).

Замечание.

Функция двух переменных z = f(x, y) может иметь множество точек разрыва; если они составляют линию, то она называется линией разрыва.

Указать точки или линии разрыва функций:

9.

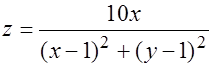
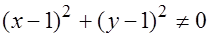в т. М₀(1, 1) функция терпит разрыв.

10.

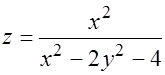
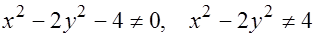
Гипербола 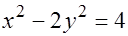является линией разрыва функции.

11.

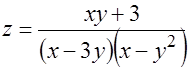
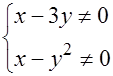
прямая 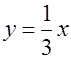и парабола 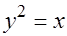являются линиями разрыва.

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.