Хелпикс

Главная

Контакты

Случайная статья



Дифференциальное исчисление функции нескольких переменных.

Стр 1 из 2Следующая ⇒


Дифференциальное исчисление функции нескольких переменных.

 

Вычисление пределов функции .

Фронтальный опрос.

1. Дать определение функции двух переменных.

2. Дать определение области определения функции двух переменных.

3. Дать определение предела функции 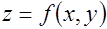 в точке .

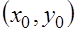4. Дать определение непрерывности функции 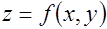: в точке 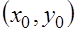; в области .

 

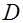1. НАХОЖДЕНИЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ ФУНКЦИИ.

 

Найти область определения функций:

1.

 

Р е ш е н и е.

Данная функция принимает действительные значения при условии

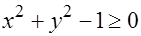, т. е. .

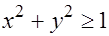Областью определения функции является часть плоскости вне единичного круга с центром в начале координат, включая окружность .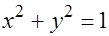

 

 

2. .

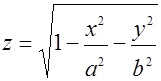Р е ш е н и е.

 


Данная функция определена при 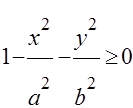, т. е. . Областью определения функции является часть плоскости, ограниченная эллипсом 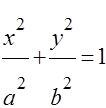, замкнутая область.

3. z = ln (y2 –­­­ 4x + 8)

Р е ш е н и е.

Функция определена при y2 –­­­ 4x + 8 > 0, т. е. y2 > 4x – 8; y2 > 4(x – 2).

Областью определения функции является часть плоскости вне параболы, за исключением точек параболы.

 

4. .

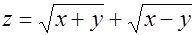Р е ш е н и е.

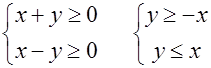
Областью определения функции является заштрихованная на рисунке часть вертикального угла, образованного биссектрисами координатных углов, включая сами биссектрисы.

5. .

Решение.

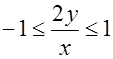
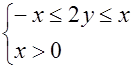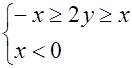или ;        или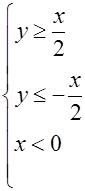

 

 

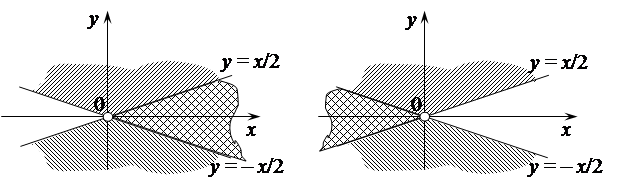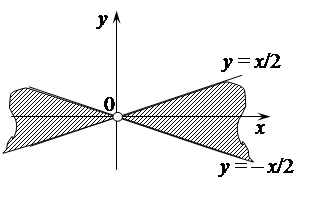     Поэтому областью определения функции является вертикальный угол, образованный прямым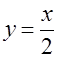и  и 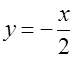, за исключением точки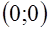

 

6. .

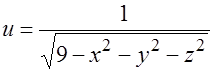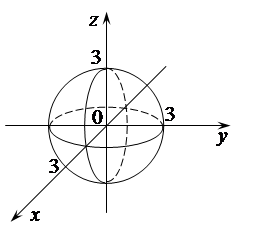Решение.

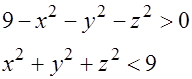
     Областью определения является множество внутренних точек шара. (Поверхность сферы не включается.)

 

 

7. .

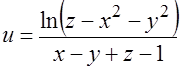Решение.

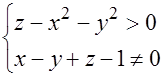
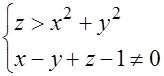
     Областью определения функции является множество точек, лежащих выше поверхности параболоида 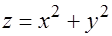, за исключением точек плоскости .

 


12Следующая ⇒
  

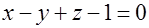© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.