Следовательно, функция принимает как наименьшее значение (при a , так и наибольшее (при a значения при x=-b/2a, и они равны в обоих случаях y=c-b2/4a.

Алгебра

Квадратичная функция. Построение графика квадратичной функции.

Рассмотрим квадратичную функцию y=ax²+bx+c.

Сделаем преобразование (выделение полного квадрата): ax²+bx+c=a(x+b/2a)²+(c-b²/4a)

Очевидно, что при a 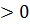a(x+b/2a)² 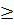0, y=a(x+b/2a)²+(c-b²/4a) 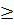(c-b²/4a), причём равенство достигается только при x=-b/2a. Значит, при x=-b/2a , функция принимает наименьшее значение y=c-b²/4a

При a 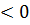a(x+b/2a)² 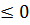и при x=-b/2a функция принимает наибольшее значение y=c-b²/4a

Следовательно, функция принимает как наименьшее значение (при a , так и наибольшее (при a значения при x=-b/2a, и они равны в обоих случаях y=c-b2/4a.

1) y=x²-7x+10; a=1, b=-7, c=10; -b/2a=7/2=3,5, c-b²/4a=10-12,25=-2/25 так как a 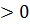, функция принимает наименьшее значение

при x=-3,5, равное y =-2,25

2) y=(-3/5)x²+(7/2)x-23; a=-3/5, b=7/2, c=-23; -b/2a=(-7/2)/(-6/5)=35/12, c-b²/4a=-23-(49/4)(-12/5)=-23+245/48=-17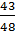

так как a 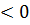, функция принимает наибольшее значение при x=35/12, равное -17

Рассмотрим теперь, как выглядит график функции y=ax2+bx+c.

Сравним его с графиком y=a(x+b/2a)², а тот в свою очередь с графиком y=ax².

Мы знаем, что график функции y=ax² представляет собой параболу.

Если на графике y=ax² лежит точка с координатами (x₀, y₀), то y₀=ax₀²

Сделаем преобразование: y₀=a((x₀-b/2a)+b/2a)²

Значит, на графике y=a(x+b/2a)² лежит точка (x₀-b/2a, y₀)

Очевидно, что множество значений {y} у функций y=a(x+b/2a)² и y=ax² совпадает, и график функции y=a(x+b/2a)² получается из графика функции y=ax² сдвигом на b/2a влево, если b/2a положительна, или вправо, если b/2a – отрицательна.

То есть графиком функции y=a(x+b/2a)² является парабола

Вершина (0, 0) параболы y=ax² переходит в вершину (-b/2a, 0) параболы y=a(x+b/2a)²

Сравним теперь графики функции y=ax²+bx+c=a(x+b/2a)²+(c-b²/4a) и функции y=a(x+b/2a)²

Очевидно, что график y=ax²+bx+c=a(x+b/2a)²+(c-b²/4a) получается из графика y=a(x+b/2a)² сдвигом на (c-b²/4a) вверх, если c-b²/4a положительна, или вниз, если c-b²/4a - отрицательна.

То есть график y=ax²+bx+c=a(x+b/2a)²+(c-b²/4a) - парабола

Вершина (-b/2a, 0) параболы y=a(x+b/2a)² переходит в вершину

(-b/2a, c-b²/4a) параболы y=ax²+bx+c=a(x+b/2a)²+(c-b²/4a).

12 Следующая ⇒