Хелпикс

Главная

Контакты

Случайная статья



АЛГЕБРА. Квадратные неравенства. Значит решением неравенства  ax2+bx+c 0 (при a ) будет множество: x1 x  x2.

Стр 1 из 2Следующая ⇒


АЛГЕБРА

Квадратные неравенства

Если в левой части неравенства стоит квадратный трёхчлен, а в правой – нуль, то такое неравенство называется квадратным.

Пример:        x2-7x+67 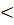 0, -3x2-56x-12  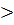0, 7x2-6  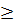0, -(1/9)x2+5x 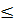0

В общем виде: ax2+bx+c 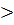0, ax2+bx+c 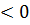,  ax2+bx+c 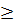0,  ax2+bx+c 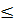0

Заметим, что если мы изменим знак a, то неравенство изменится на противоположное. Поэтому будем считать, что a положительное.

Для решения квадратного неравенства любого вида сначала решим квадратное уравнение ax2+bx+c=0

А) Пусть у него два различных корня x1 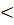x2

Тогда по теореме на стр. 182 существует разложение ax2+bx+c=a(x-x1)(x-x2)

Если ax2+bx+c 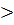0, то  a(x-x1)(x-x2) 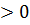, и так как a 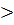0, то это выражение положительно, если, либо оба множителя положительны, либо оба – отрицательны. Значит, неравенство сводится к системам линейных неравенств:

x-x1 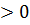      или      x-x1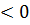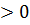

 x-x2                     x-x2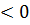

Так как x1 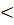 x2, то решением первой системы будет множество x  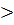x2, а решением второй - множество x  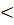x1.

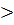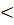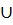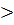 Таким образом решением неравенства ax2+bx+c 0 (при a ) будет объединение множеств x  x1  x  x2

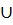(  можно заменить на «или»)

Если же ax2+bx+c 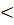0 , то a(x-x1)(x-x2) 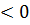. Тогда система будет такой:

x-x1 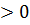            или                x-x1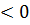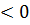

x-x2                           x-x2 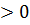Оба множителя должны быть разных знаков.

Так как x1 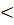 x2 , то решением первой системы будет:  x1 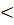x 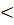 x2, а вторая система не имеет решений.

Значит решением неравенства  ax2+bx+c 0 (при a ) будет множество: x1 x  x2.

654) (6) 3x2+2x-1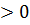

Решаем сначала уравнение: 3x2+2x-1=0. Его корнями будут x1=1/3, x2=-1

Преобразуем неравенство: 3(x-1/3)(x+1)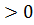   

x-1/3 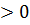                           или          x-1/3<0                    

x+1 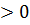                                                  x+1<0  

 

Решением первой системы будет: x 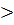1/3, а решением второй: x<-1                Значит, решение неравенства: x<-1 или x>1/3

Рассмотрим случай с отрицательным a: -(1/5)x2+3x-10>0

Поменяем знак:

(1/5)x2-3x+10<0,

Решим уравнение: (1/5)x2-3x+10=0 x1=5, x2=10

Значит, (1/5)(x-5)(x-10)<0. Множители должны быть разных знаков:

x>5                             x<5

x<10                           x>10

Решением первой системы будет: 5<x<10. Вторая система решений не имеет.

Значит решением неравенства будет: 5<x<10.


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.