Угол поворота

Единичная окружность — это окружность, радиус которой принят за единицу измерения.

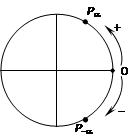
Числовая окружность — это единичная окружность с установленным соответствием между действительными числами и точками окружности:

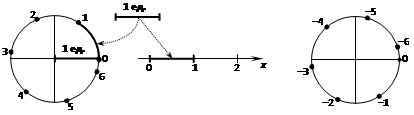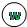Указанное соответствие можно определить следующим образом: каждому числу a соответствует такая точка Р числовой окружности, чтобы дуга ÈОР имела длину |a| и была отложена в положительном направлении если a > 0 и в отрицательном, если a < 0:

Признаки числовой окружности:

1) начало отсчета – правый конец горизонтального диаметра;

2) единичный отрезок – длина радиуса окружности;

3) положительное направление – против часовой стрелки.

Откладывать можно дуги какой угодно длины. То есть числовую окружность можно рассматривать как окружность радиуса 1, на которую «намотана» числовая прямая:

Радианная мера углов и дуг

Угол в 1° — это центральный угол, опирающийся на дугу, длина которой равна части окружности.

Угол поворота — это угол, полученный вращением луча около его начала О от начального положения ОА до конечного положения ОВ.

Угол в 1 радиан — это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.

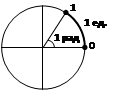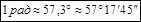
Радианная мера угла численно равна пути, который проходит точка по дуге единичной окружности, на которую опирается этот угол:

Для связи радианов и градусов используют развернутый угол:

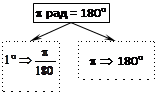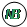1. Говорят: «угол радиан» или чаще «угол ». Обозначение «радиан» или «рад», как правило, опускают.

2. Термин «радианное измерение углов» равносилен термину «числовое измерение углов», т.е. фраза «угол a равен двум радианам» равносильна фразе «угол a равен числу 2» и даже «угол a равен двум». Поэтому вопрос типа «Чему равно ?» некорректен. Нужно спрашивать: «Чему равен угол ?» (60°) или «Чему равно число ?» (» 1,05).

Угол поворота

áПолныйñ оборот — это угол поворота, равный 2p рад (или 360°).

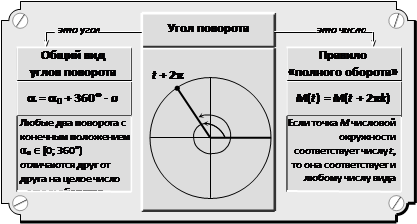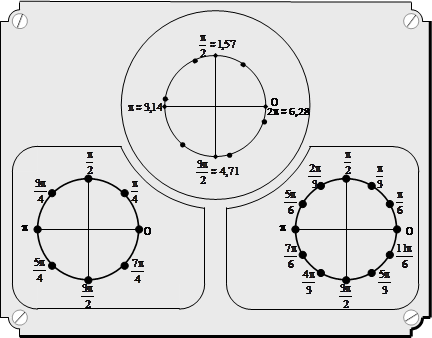
Некоторые положения конечной точки угла поворота:

12 3 Следующая ⇒