
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Алгебра. Распределительный закон. а · (в + с) = а · в + а · с. а · а · … · а = аn, а0 = 1, а1 = а, где n Q. Вероятность и статистика. Основное свойство дроби. Пропорция. Арифметическая прогрессия. Формулы сокращенного умножения. Раскрытие скобок. Геометри
Алгебра
Распределительный закон
а · (в + с) = а · в + а · с
 Степени и корни
Степени и корни
а · а · … · а = аn, а0 = 1, а1 = а, где n Q
n - раз
1)  an · am = an + m 4) an · bn = (a·b)n
an · am = an + m 4) an · bn = (a·b)n
2) an : am = an – m 5) 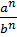 =
= 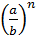 ,b ≠ 0
,b ≠ 0
3) (an)m = an·m. 6) 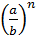 =
= 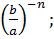
7) 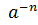 =
=  ; 8)
; 8) 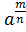 =
= 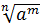 ;
;
9) 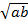 =
= 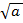 ·
· 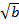 ; 10)
; 10) 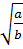 =
= 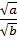

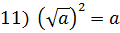 , 12)
, 12) 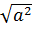 = |a|.
= |a|.
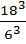 =
=  ;
; 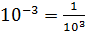 =0, 001
=0, 001
3 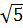 =
= 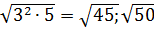 =
= 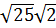 = =5
= =5 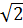 ;
; 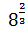 =
= 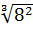 =
= 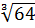 =4
=4
Вероятность и статистика
P =  , P = 1 -
, P = 1 - 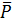
P = P1 + P2 (или),
P = P1 ∙ P2 (и)
Основное свойство дроби
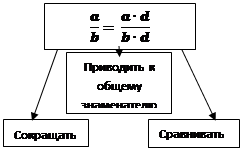
Пр. 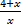 = не сокращ!
= не сокращ! 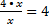
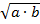 Медиана (Ме) – cреднее арифм. минус число стоящее посредине ранжированного ряда.
Абсолютная погрешность
Медиана (Ме) – cреднее арифм. минус число стоящее посредине ранжированного ряда.
Абсолютная погрешность
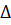 х =|хист - хизм|
х =|хист - хизм|
Пропорция
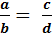 , ad = bc(b,d
, ad = bc(b,d 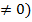
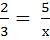 , 2х = 3∙5, х = 7,5
, 2х = 3∙5, х = 7,5
1 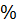 - сотая часть числа.
- сотая часть числа.
Задачи на 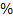 реш. через пропорцию.
реш. через пропорцию.
Арифметическая прогрессия
an+1 = an + d
an= a1 + (n – 1)d.
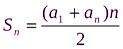
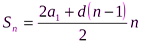
Формулы сокращенного умножения
(a + b)(a – b) = a2 – b2
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
Раскрытие скобок
2 – (– х + 3) = 2 + х – 3 = х – 1;
5ab - 3b(2 + a) = 5ab - 6b – 3ba = =2ab - 6b
Геометрическая прогрессия
bn+1 = bn∙q,
bn= b1∙qn-1.
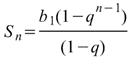
Cокращение дробей
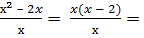 х – 2;
х – 2;
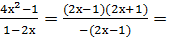 (2х+1)
(2х+1)
a + a = 2a, 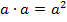
Решение неполного квадратного уравнения
Решение полного квадратного уравнения
 ах2 + с = 0, с ≠ 0
ах2 + с = 0, с ≠ 0
ах2 + bх = 0, в ≠ 0
ах2 + bx + с = 0, с ≠ 0, а ≠ 0
х2 = d, d ≠ 0
x1,2 = 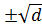 ,
,
х(ах + b) = 0
х1 = 0, ах + b = 0
x = -  .
.
D = – дискриминант, х1,2 = .
Теорема Виета: х2 + pх + q = 0, то х1 + х2 = - p, х1· х2 = q.
ах2 + bх + с = а(х – х1)(х – х2), где х1, х2– корни.
Стандартный вид числа.
0,012 = 1,2 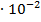 ; 2370 =2,37∙103
; 2370 =2,37∙103
 289
289

 Функции и графики
Функции и графики
 Линейная функция у = kx + b
Линейная функция у = kx + b


 y = -x y = 2x y = x
y = -x y = 2x y = x
y = 1
k = 1 стандарт
k> 1 ветви выше к оси ОY
0 <k< 1 ветви ниже к оси ОХ
k< 0 отражение отн. оси ОХ
b> 0 сдвиг вверх
b< 0 сдвиг вниз


 Парабола y = ax2+bx + c
Парабола y = ax2+bx + c
D< 0
D = 0
y=х2 D> 0
 | |||
 | |||
 x1 x2
x1 x2
 c
c
 (x0;y0)
(x0;y0)
а = 1 стандарт
а > 1 ветви уже ветви вверх
0 <a< 1 ветви шире
a< 0 ветви вниз
x0 =  , y0 = f(x0)
, y0 = f(x0)
 Гипербола y =
Гипербола y = 
 | |||
 | |||
 1
1

 -1 1
-1 1
 -1
-1
k = 1 стандарт
k> 1 ветви шире
0 <k< 1 ветви уже
k< 0 отражение отн. оси ОХ