
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Ортонормированный базис.. Координаты вектора в ортонормированном базисе.. Скалярное произведение векторов.
2. Ортонормированный базис.
Определение: Базис называется ортонормированным, если:
1). Вектора взаимно перпендикулярны (орто);
2). Их длины =1 (норма).
Пример: 
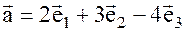 ; Пусть:
; Пусть:
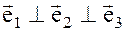
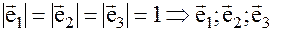 - образуют ортонормированный базис. Координаты вектора
- образуют ортонормированный базис. Координаты вектора 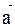 в этом базисе:
в этом базисе: 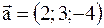 .
.
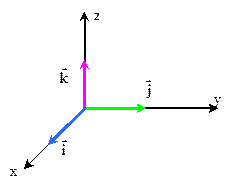 |
Определение: Система координат с ортонормированным базисом
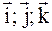 называется прямоугольной декартовой системой координат.
называется прямоугольной декартовой системой координат.
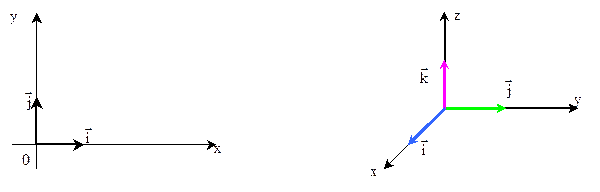 |
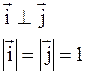
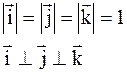
Вывод: 
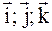 - всегда базис ортонормированный.
- всегда базис ортонормированный.
3. Координаты вектора в ортонормированном базисе.
Теорема: Координаты вектора в прямоугольной декартовой системе координат равны проекциям этого вектора на оси координат.
Док-во: 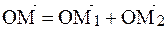 ;
; 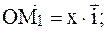
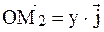 ;
; 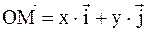 , где
, где 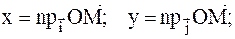 или
или 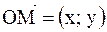 .
.
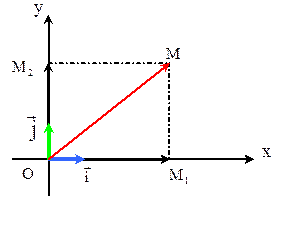 | 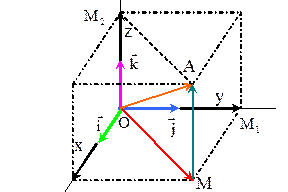 | ||
Рассмотрим пространственную систему координат XYZ и вектор
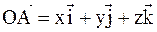 , который равен сумме векторов
, который равен сумме векторов 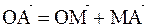 , где координаты вектора есть
, где координаты вектора есть 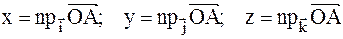 или вектор
или вектор 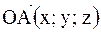 -в ортонормированном базисе.
-в ортонормированном базисе.
4. Скалярное произведение векторов.
Определение: Скалярным произведением векторов 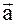 и
и 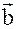 называется число, равное произведению длин этих векторов на косинус угла между ними.
называется число, равное произведению длин этих векторов на косинус угла между ними.
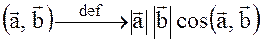
 Свойства скалярного произведения векторов:
Свойства скалярного произведения векторов:
 1.
1. 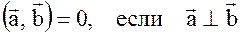
 2.
2. 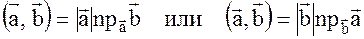
 Док-во:
Док-во:

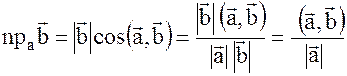 или
или 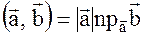 и аналогично можно показать второе.
и аналогично можно показать второе.
3. 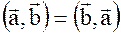
4. 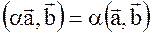
5. 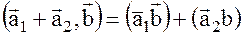 Док-во:
Док-во:
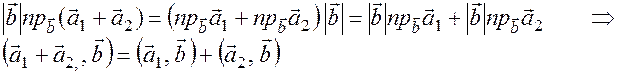
6. 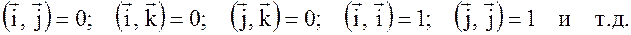
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|