
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция 8.. Декартовая система координат. Разные задачи.. Ортонормированный базис.. Координаты вектора в ортонормированном базисе.. Скалярное произведение векторов.
Лекция 8.
План:
1) Декартовая система координат. Разные задачи.
2) Ортонормированный базис.
3) Координаты вектора в ортонормированном базисе.
4) Скалярное произведение векторов.
Определение: Декартовой системой координат называется совокупность точки – начала координат и базисных векторов.
Замечание: Декартовая система координат может быть прямоугольной или косоугольной, которую ещё называют аффинной.
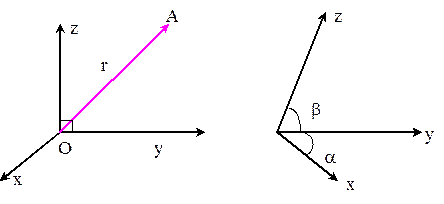 |
Определение: Вектор, начало которого совпадает с началом системы координат, называется радиус вектором.
Задача 1:Пусть задана декартовая система координат точка О и базис 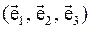 и пусть радиус-вектор
и пусть радиус-вектор 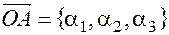 , а радиус-вектор
, а радиус-вектор
|

 . Найдём вектор
. Найдём вектор 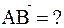
Задача 2: Деление отрезка в данном отношении.
Найти координаты точки M(x; y; z) на отрезке AB, которая делит отрезок в отношении 
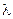 ; Известны точки
; Известны точки 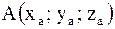 и
и 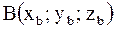 .
.
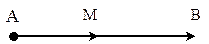
Решение:
Известно: что 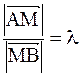 , тогда, согласно теореме 1, (из предыдущей лекции) имеем
, тогда, согласно теореме 1, (из предыдущей лекции) имеем  , (т. к.
, (т. к.  ).
).
Согласно формуле (1) найдём координаты вектора 
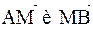 ;
; 
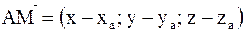
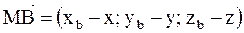
Согласно теореме 4, т.к. 
 получим:
получим: 
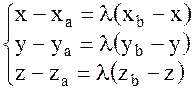 преобразуем и найдём: x; y; z.
преобразуем и найдём: x; y; z.
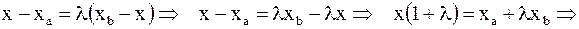 имеем:
имеем:
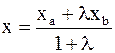
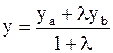 (2)
(2)
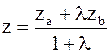
Задача 3: Проекция вектора на ось.
Определение: Прямая, с заданным на ней базисным вектором  называется осью. Рассмотрим ортогональную проекцию вектора на ось.
называется осью. Рассмотрим ортогональную проекцию вектора на ось.
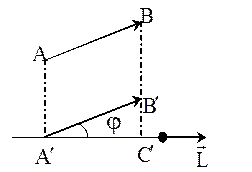 |
Ортогональная проекция:

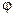 - угол между вектором
- угол между вектором 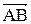 и осью
и осью  .
.
Замечание: По аналогии найдём проекцию вектора 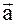 на вектор
на вектор 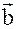 в виде:
в виде: 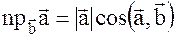 .
.
Теорема: Проекция суммы векторов на ось равна сумме проекций слагаемых векторов на эту ось.
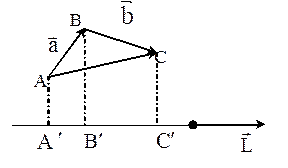 |
Покажем на рисунке:
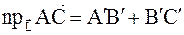
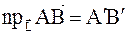
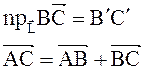
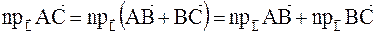
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
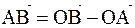 ; Согласно теореме 4 при вычитании векторов вычитаются координаты
; Согласно теореме 4 при вычитании векторов вычитаются координаты 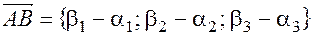 (1)
Правило: Для нахождения координат вектора из координат конечной точки надо вычесть координаты начальной точки.
(1)
Правило: Для нахождения координат вектора из координат конечной точки надо вычесть координаты начальной точки.