
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Векторная алгебра.. Демонстрационный пример решения контрольной работы.. записать векторы в системе орт и найти модули этих векторов;. найти угол между векторами и ;. найти проекцию вектора на вектор ;. найти площадь грани ABC; . найти объем пирамиды
Векторная алгебра.
1. Демонстрационный пример решения контрольной работы.
Даны координаты вершины пирамиды АВСD:
А(5; -3;1), В(0;2;6), С(-1; 4;7), D( 3;-6;5).
Требуется:
1) записать векторы в системе орт и найти модули этих векторов;
2) найти угол между векторами и ;
3) найти проекцию вектора на вектор ;
4) найти площадь грани ABC;
5) найти объем пирамиды ABCD.
Решение:
1) Запись вектора в системе орт имеет вид 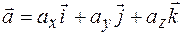 , где
, где 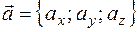 координаты вектора,
координаты вектора, 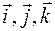 орты осей Ох, Oy, Oz соответственно.
орты осей Ох, Oy, Oz соответственно.
Длина или модуль вектора находится по формуле  .
.
Найдем координаты вектора 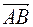 по формуле
по формуле
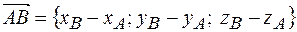 , тогда
, тогда
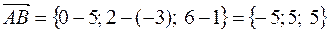
или в системе орт 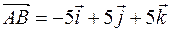 .
.
Модуль вектора 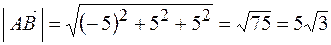 .
.
Аналогично, координаты вектора 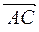 находим по формуле
находим по формуле
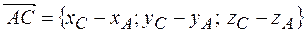 , тогда
, тогда
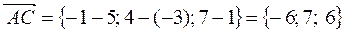
или в системе орт 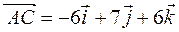 .
.
Модуль вектора 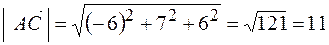 .
.
Найдем координаты вектора 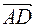 по формуле
по формуле
 , тогда
, тогда
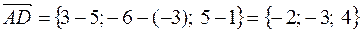
или в системе орт 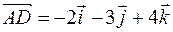 .
.
Модуль вектора 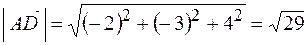 .
.
2)Определение. Скалярным произведением 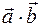 векторов
векторов 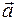 и
и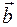 называется число, равное произведению модулей векторов
называется число, равное произведению модулей векторов 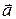 и
и 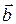 на косинус угла между ними:
на косинус угла между ними: 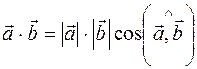
Теорема.Скалярное произведение векторов 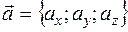 и
и 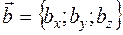 вычисляется по формуле:
вычисляется по формуле: 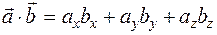 .
.
Скалярное произведение позволяет находить угол между векторами, координаты которых известны. Из определения скалярного произведения имеем:
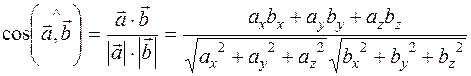 .
.
Найдем угол между векторами  и
и 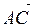 , где
, где
 и
и 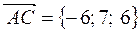

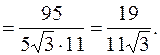
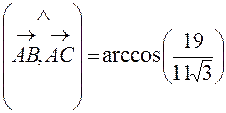 .
.
3) Скалярное произведение позволяет находить проекцию вектора на вектор
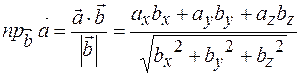
Найдем проекцию вектора 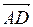 на вектор
на вектор  , где
, где  и
и 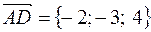 .
.
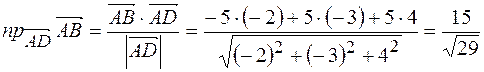
4) Определение. Векторным произведением 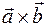 векторов
векторов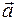 и
и 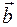 называется вектор
называется вектор 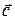 такой, что:
такой, что:
1) 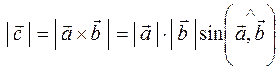 ;
;
2) 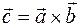 перпендикулярен к плоскости векторов
перпендикулярен к плоскости векторов 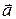 и
и 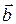 ;
;
3) 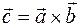 образует с упорядоченной парой векторов
образует с упорядоченной парой векторов 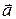 и
и 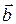 правую тройку (т.е. если смотреть с конца вектора
правую тройку (т.е. если смотреть с конца вектора 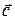 на плоскость векторов
на плоскость векторов 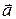 и
и 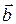 , то кратчайший поворот от вектора
, то кратчайший поворот от вектора 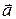 к вектору
к вектору 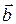 происходит против часовой стрелки).
происходит против часовой стрелки).
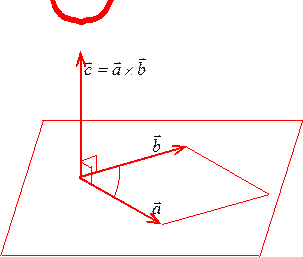
Геометрический смысл векторного произведения. Модуль векторного произведения 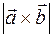 численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах 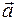 и
и 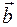 .
.
Теорема. Векторное произведение векторов  и
и 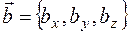 вычисляется по формуле:
вычисляется по формуле:
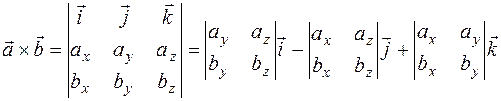 .
.
Найдем площадь грани ABC, как треугольника, построенного на векторах
 и
и 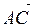 , где
, где 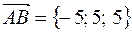 и
и 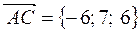 .
.
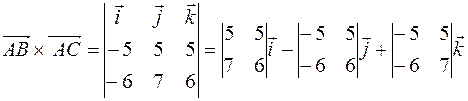
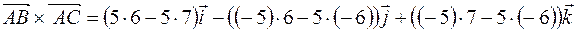
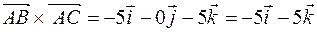
Модуль 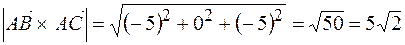 .
.
Площадь треугольника ABC равна 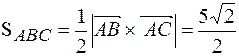 .
.
5) Смешанное произведение 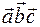 .
.
Теорема. Пусть 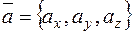 ,
, 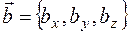 ,
, 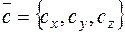 . Тогда
. Тогда
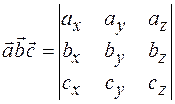 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|