
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Скалярное произведение векторов, его свойства и приложения
Скалярное произведение векторов, его свойства и приложения
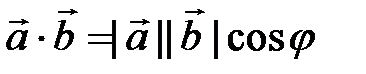 ,
,
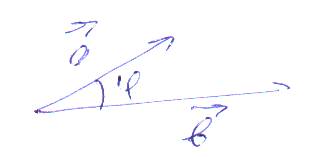
Основные свойства скалярного произведения:
1) 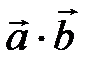 =
= 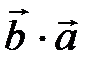 ;
;
2) 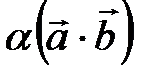 =
= 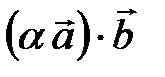 =
= 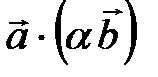 ,
, 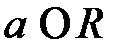 ;
;
3) 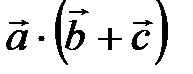 =
= 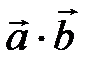 +
+ 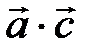
4) 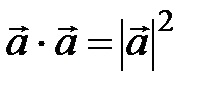 , отсюда
, отсюда 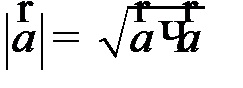 . В частности
. В частности  ;
;
5) 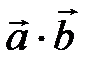 =0
=0 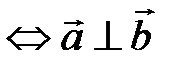 , в частности
, в частности 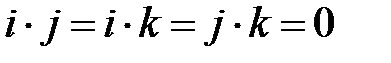 .
.
Таблица скалярного произведения базисных векторов 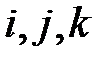 .
.
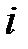
| 
| 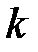
| |
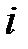
| |||

| |||
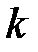
|
Выражение скалярного произведения через координаты
Пусть даны два вектора 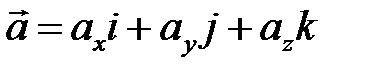 и
и 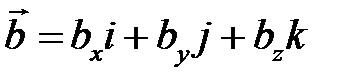 .
.
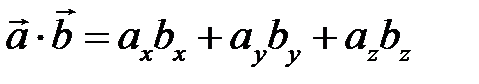
Некоторые приложения скалярного произведения
1. Угол между векторами
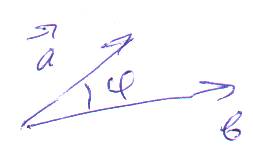
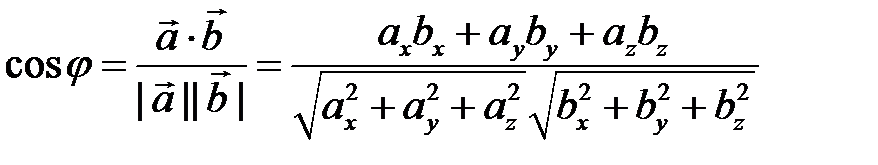 .
.
Отсюда следует, что если 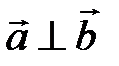 , то
, то 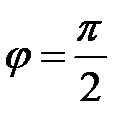 а
а 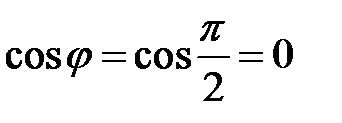 и соответственно
и соответственно
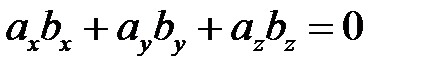
есть условие ортогональностивекторов в координатах.
Векторное произведение векторов, его свойства и приложения
Определение. Векторным произведением вектора  на вектор
на вектор 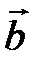 называется вектор
называется вектор 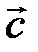 , который:
, который:
1) ортогонален векторам  и
и 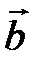 , т.е.
, т.е. 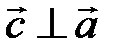 ,
, 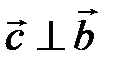 ;
;
2) имеет длину равную 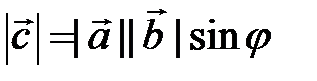 , где
, где 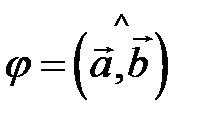 ,
, 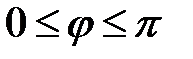 ,
,
т.е. численно равен площади параллелограмма, построенного на векторах  и
и 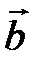 как на сторонах;
как на сторонах;
3) векторы  ,
, 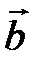 и
и 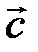 образуют правую тройку.
образуют правую тройку.
Геометрически
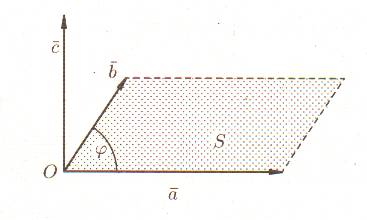
Векторное произведение обозначается 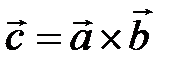 или
или 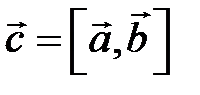 .
.
Основные свойства векторного произведения:
1) 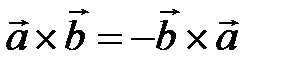 ;
;
2) 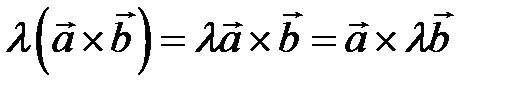 ,
, 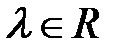 ;
;
3)  ×
× 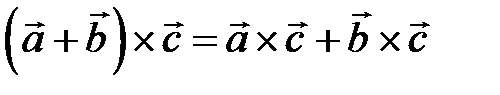 ;
;
4) если 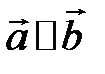 , то
, то 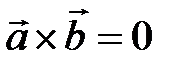 (если векторы коллинеарны, то их векторное произведение равно нулю), в частности
(если векторы коллинеарны, то их векторное произведение равно нулю), в частности  .
.
Таблица векторного произведениями базисных векторов 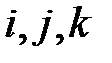
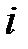
| 
| 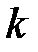
| |
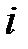
| 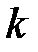
| 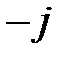
| |

| 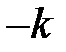
| 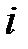
| |
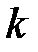
| 
| 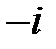
|
Выражение векторного произведения через координаты
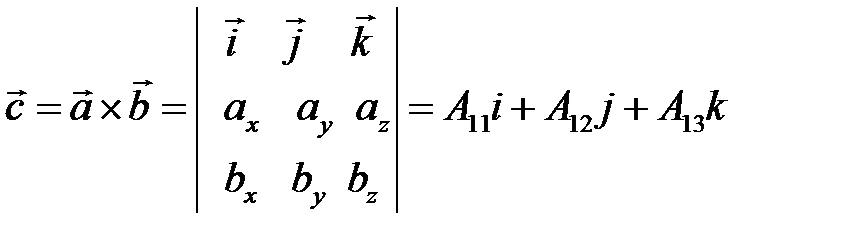
Некоторые приложения векторного произведения
1) Установление коллинеарности
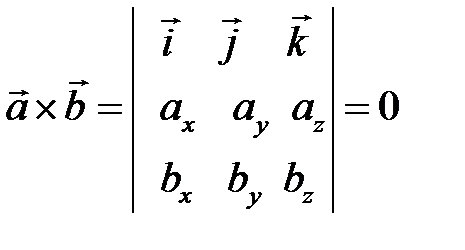 .
.
Следовательно, две строки пропорциональны, т.е 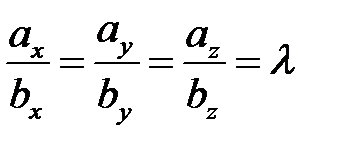 , т.е векторы коллинеарны.
, т.е векторы коллинеарны.
2) Нахождение площадей параллелограмма и треугольника
Согласно определению векторного произведения
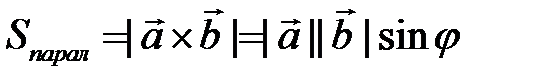 ,
,
где векторы 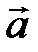 и
и  - стороны параллелограмма
- стороны параллелограмма
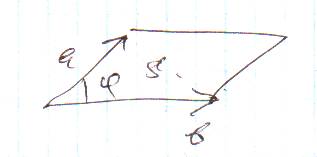
Соответственно площадь треугольника

есть
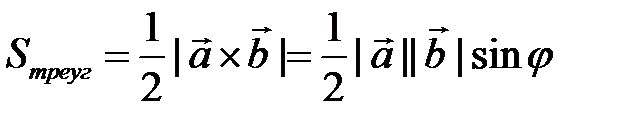 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|