Ответ1=Функция(Сглаживание(1..30),Сглаживание(2..31))

Ответ1=Функция(Сглаживание(1..30),Сглаживание(2..31))

Хотелось бы получить программу без необоснованно излишних повторных вычислений и необоснованно излишнего перерасхода памяти (объема зависящего от длины последовательности).

--------------------------------------------------------------------------------------------

«Переменная» – символ в алфавите a..z. «Имя функции» – символ в алфавите A..Z. Размерность функций (количество аргументов) задана массивом R: ARRAY[‘A’..’Z’] OF 0..50

Определение понятия «Терм» (выражение в префиксной записи):

§ «Переменная» есть «Терм».

§ Если F - «ИмяФункции» размерности k, а t₁,t₂...t_k - «Термы», то Ft₁t₂…t_k – тоже «Терм», причем t₁,t₂...t_k (и их подтермы) называются его подтермами (подвыражениями).

Для заданной (вводом) последовательности символов, являющейся «Термом», и заданного (вводом) символа в алфавите «Имен функций» выделить первый (слева) подтерм, начинающийся с этого «Имени функции», т.е. вывести его в выходной поток.

ПРИМЕР. Пусть F,G,H – функции размерности 1,2,3 соответственно.

Терм: GFGxHxFyGHHFxyzFyyxz

Обычно его пишут так: G(F(G(x,H(x,F(y),G(H(H(F(x),y,z),F(y),y),x)))),z)

Жирным подчеркнутым курсивом выделен первый подтерм, начинающийся с H

--------------------------------------------------------------------------------------------

Разреженная (с большим количеством нулевых элементов) матрица A[N][N] представлена вектором троек (i,j,a[i][j]) для всех (i,j) таких, что A[i][j]≠0 (пусть их K штук). Разреженная матрица B[N][N] представлена аналогично вектором троек (пусть их L штук).

Надо вычислить произведение A на B, представленное аналогично вектором троек, их получится ≤N*N, но надо вычислить M - сколько конкретно их получится. Поскольку элементы произведения получаются в порядке по строкам, умножением строки из A на столбец из B, пусть:

§ ненулевые элементы матрицы A выписаны в вектор в порядке по строкам матрицы A (и слева направо в строке), аналогично надо разместить ненулевые элементы произведения;

§ ненулевые элементы матрицы B выписаны в вектор в порядке по столбцам матрицы B (и сверху вниз в столбце).

Конечно, можно сначала восстановить матрицы A и B по их векторному представлению, перемножить и построить уплотнённое представление произведения, но это банальное решение интереса не представляет. Хотелось бы вычислить произведение аккуратнее - не перебирая (отсутствующие) нулевые элементы перемножаемых матриц. Исходные данные – перемножаемые матрицы в векторном представлении, их ввод не нужен, вывод произведения тоже не нужен.

--------------------------------------------------------------------------------------------

Схема дорог между N городами описана матрицей S:ARRAY[1..N,1..N]OF 0..1, где S[i,j]=S[j,i]=1, когда i-й и j-й города непосредственно связаны дорогой, и =0 иначе. Например:

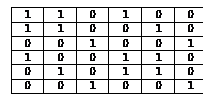
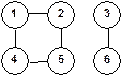Можно ли из любого города проехать в любой другой? Проверить это можно, «склеивая» пары городов (i,j), непосредственно связанные дорогой, т.е. в матрице проставив дополнительные единицы показывающие, что i-й город непосредственно связан дорогой с каждым городом, с которым непосредственно связан j-й город (и наоборот). Ответ на поставленный вопрос будет положительным, если таким образом можно «склеить» все города в один. Составить программу проверки - можно ли из любого города проехать в любой другой, для заданной матрицей схемы дорог между ними. Отметим, что фактически достаточно начинать с (любого) одного из городов, например первого, и все другие пытаться «вклеивать только в него».

⇐ Предыдущая 12