Хелпикс

Главная

Контакты

Случайная статья



Определения: 1.  Если определитель матрицы ≠ 0, то матрица называется невырожденной или неособенной.

Стр 1 из 4Следующая ⇒


 

 «ОБРАТНАЯ МАТРИЦА».

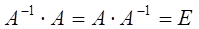
Определение: Матрица 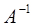 называется обратной по отношению к квадратной матрице 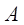, если при умножении матрицы  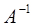на матрицу  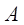как справа, так и слева, получается единичная матрица, т. е. имеет место равенство:

 

Замечания: 1. Только квадратная матрица имеет обратную.

                 2. Матрица, обратная данной, тоже квадратная.

 

Определения: 1.  Если определитель матрицы ≠ 0, то матрица называется невырожденной или неособенной.

2.Если определитель матрицы =0, то матрица называется вырожденной или особенной.

3. Присоединенная матрица 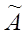 («А с волной»), получается из матрицы 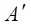, транспонированной по отношению к матрице 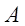, заменой элементов матрицы  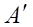на их алгебраические дополнения.

 

Теорема (необходимое и достаточное условие существования обратной матрицы):

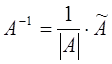
Обратная матрица 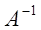 существует и единственна тогда и только тогда, когда матрица  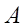невырожденная, т.е. 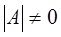. Ее элементы вычисляются по формуле:

 

«ОБРАТНАЯ МАТРИЦА».

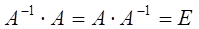
Определение: Матрица 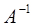 называется обратной по отношению к квадратной матрице 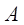, если при умножении матрицы  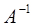на матрицу  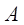как справа, так и слева, получается единичная матрица, т. е. имеет место равенство:

 

Замечания: 1. Только квадратная матрица имеет обратную.

                 2. Матрица, обратная данной, тоже квадратная.

 


1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.