Задачи для самостоятельной работы

Задачи для самостоятельной работы

Задача 6

Доказать, что биссектриса внешнего угла треугольника пересекает продолжение противоположной стороны в точке, расстояния от которой до концов этой стороны пропорциональны прилежащим сторонам треугольника [М.И.Лисова,О.Н.Пирютко, Планиметрия. Итоговое повторение, №3.06, стр.48].

Задача 7

В треугольнике ABC известно , что BC=12 cm, AC=8 cm и уголA вдвое больше угла B. Найдите AB [М.И.Лисова,О.Н.Пирютко, Планиметрия. Итоговое повторение, №3.07, стр.50].

Задача 8

На высотах BB₁ и CC₁ треугольника ABC взяты точки B₂ и C₂ так, что 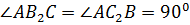[М.И.Лисова,О.Н.Пирютко, Планиметрия. Итоговое повторение, №3.08, стр.51].

Докажите, что AB₂=AC₂.

Задача 9

На стороне BC треугольника ABC взята точка A₁ так, что BA₁:A₁C=2:1. В каком отношении медиана CC₁ делит отрезок AA₁ [М.И.Лисова,О.Н.Пирютко, Планиметрия. Итоговое повторение, №3.09, стр.52].

Задача 10

В треугольнике ABC отрезки AD и BE, проведены к сторонам BC и AC соответственно, делят точкой пересечения в следующем отношении , где Q=AD . В каком отношении E и D делят стороны треугольника? [М.И.Лисова,О.Н.Пирютко, Планиметрия. Итоговое повторение, №3.13, стр.56].

⇐ Предыдущая 12