
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
сСтатическая устойчивость системы
81.5. сСтатическая устойчивость системы
при работе станции на шины
соизмеримой мощности
Pacсмотрим систему электропередачи,на приемном конце которой наряду с нагрузкой имеется местная электростанциямощностью, соизмеримой смощностью электропередачи (рис. 81.12, а).
8.5. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ СИСТЕМЫ
ПРИ РАБОТЕ СТАНЦИИ НА ШИНЫ
СОИЗМЕРИМОЙ МОЩНОСТИ
 |
Pacсмотрим систему электропередачи,на приемном конце которой наряду с нагрузкой имеется местная электростанциямощностью, соизмеримой смощностью электропередачи (рис. 8.12, а). Частным случаем такой системы будет резервная или автономная электростанция с двумя генераторами соизмеримой мощности, работающими на общую нагрузку. Очевидно, что в последнем случае сопротивление линии электропередачи с трансформаторами ХТЛ будет стремиться к нулю.
Будемполагать, что ЭДС обеихэлектростанций Е1 и Е2 постоянны по величине, т.е. исключим влияние регуляторов возбуждения. Тогда схема замещения (рис. 81.12, б) и режим работы этой системы станут практически аналогичны схеме замещения и режиму рассмотренной в предыдущем параграфе системы (см. рис. 81.81, а…–в). Увеличение угла 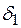 между ЭДС передающей электростанции Е1и напряжением приемника U, а следовательно и угла
между ЭДС передающей электростанции Е1и напряжением приемника U, а следовательно и угла 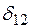 между ЭДС Е1 и Е2 (рис., 81.12, в) будет сопровождаться уменьшением напряжения во всех промежуточных точках системы, но на этот раз начнет уменьшаться и напряжение на шинах приемника U, которое в рассматриваемых условиях является некоторой промежуточной точкой в схеме замещения электропередачи.
между ЭДС Е1 и Е2 (рис., 81.12, в) будет сопровождаться уменьшением напряжения во всех промежуточных точках системы, но на этот раз начнет уменьшаться и напряжение на шинах приемника U, которое в рассматриваемых условиях является некоторой промежуточной точкой в схеме замещения электропередачи.
Таким образом, если мощность приемной системы соизмерима с мощностью электропередачи, напряжение на шинах приемника не будет оставаться постоянным при изменении режима работы электропередачи, что необходимо принимать во внимание при построении характеристики передаваемой мощности. Для учета этого изменения построим семейство синусоидальных характеристик мощности  (рис. 81.12, г) , каждая из которых отвечает различным
(рис. 81.12, г) , каждая из которых отвечает различным
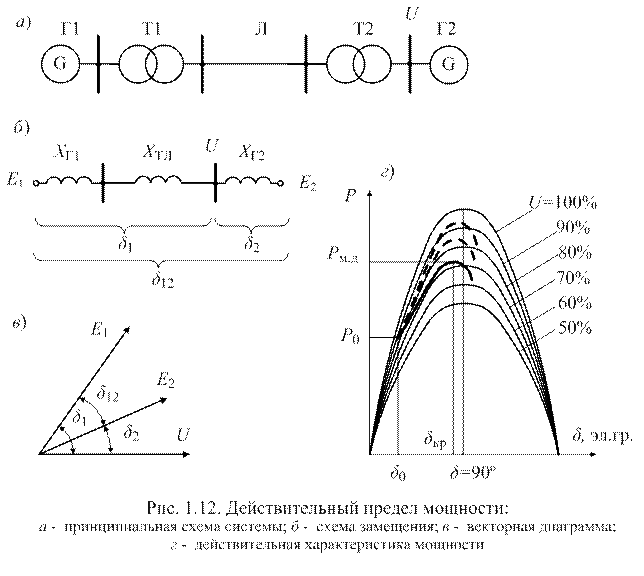
Будемполагать, что ЭДС обеихэлектростанций Е1 и Е2 постоянны по величине, т.е. исключим влияние регуляторов возбуждения. Тогда схема замещения (рис. 8.12, 6б) и режим работы этой системы станут практически аналогичны схеме замещения и режиму рассмотренной в предыдущем параграфе системы (см. рис. 8.8, а–в). Увеличение угла 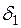 между ЭДС передающей электростанции Е1и напряжением приемника U, а следовательно и угла
между ЭДС передающей электростанции Е1и напряжением приемника U, а следовательно и угла  между ЭДС Е1 и Е2 (рис, 8.12, в) будет сопровождаться уменьшением напряжения во всех промежуточных точках системы, но на этот раз начнет уменьшаться и напряжение на шинах приемника U, которое в рассматриваемых условиях является некоторой промежуточной точкой в схеме замещения электропередачи.
между ЭДС Е1 и Е2 (рис, 8.12, в) будет сопровождаться уменьшением напряжения во всех промежуточных точках системы, но на этот раз начнет уменьшаться и напряжение на шинах приемника U, которое в рассматриваемых условиях является некоторой промежуточной точкой в схеме замещения электропередачи.
Таким образом, если мощность приемной системы соизмерима с мощностью электропередачи, напряжение на шинах приемника не будет оставаться постоянным при изменения изменении режима работы электропередачи, что необходимо принимать во внимание при построении характеристики передаваемой мощности. Для учета этого изменения построим семейство синусоидальных характеристик мощности 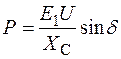 (рис. 8.12, г), каждая из которых отвечает различным значениям напряжения (при одной и той же величине ЭДС Е1). При увеличении угла
(рис. 8.12, г), каждая из которых отвечает различным значениям напряжения (при одной и той же величине ЭДС Е1). При увеличении угла 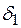 (т. е. при возрастании передаваемой мощности) напряжение на приемных шинах будет уменьшаться. Отмечая пересечения вертикалей, проведенных через определенные значения угла
(т. е. при возрастании передаваемой мощности) напряжение на приемных шинах будет уменьшаться. Отмечая пересечения вертикалей, проведенных через определенные значения угла 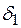 , с синусоидами характеристик мощности, соответствующих величинам напряжения U при этих значениях угла
, с синусоидами характеристик мощности, соответствующих величинам напряжения U при этих значениях угла 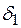 , получим так называемую действительную характеристику мощности. Максимум этой характеристики называется действительным пределом мощности Рm.м.ид. Как видно из рис. 81.12, г, вследствие возрастающего падения напряжения на шинах приемника U действительный предел мощности достигается при угле
, получим так называемую действительную характеристику мощности. Максимум этой характеристики называется действительным пределом мощности Рm.м.ид. Как видно из рис. 81.12, г, вследствие возрастающего падения напряжения на шинах приемника U действительный предел мощности достигается при угле 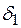 < 90°, а его величина меньше идеального предела мощности Рм.идРm.ид, соответствующего исходному режиму (U=100%).
< 90°, а его величина меньше идеального предела мощности Рм.идРm.ид, соответствующего исходному режиму (U=100%).
 Таким образом, снижение напряжения на шинах приемника соизмеримой мощности является фактором ухудшения статической устойчивости системы. Учитывая важность этого фактора, на практике часто строят характеристику передаваемой мощности в функции напряжения приемника U, а не угла
Таким образом, снижение напряжения на шинах приемника соизмеримой мощности является фактором ухудшения статической устойчивости системы. Учитывая важность этого фактора, на практике часто строят характеристику передаваемой мощности в функции напряжения приемника U, а не угла 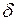 .
.
 Такая зависимость может быть легко построена по обычной угловой характеристике мощности, поскольку каждой ее точке отвечает отвечают определенные значения мощности Р и напряжения U. Откладывая по оси ординат значения U, а по оси абсцисс – соответствующие значения мощности Р, получаем характеристику U=f(P)(рис. 81.13). Линия
Такая зависимость может быть легко построена по обычной угловой характеристике мощности, поскольку каждой ее точке отвечает отвечают определенные значения мощности Р и напряжения U. Откладывая по оси ординат значения U, а по оси абсцисс – соответствующие значения мощности Р, получаем характеристику U=f(P)(рис. 81.13). Линия 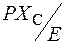 представляет собой линию идеальных пределов мощности при различных значениях напряжения U. В частности, исходному режиму (U=100%) соответствует точка b b на этой линии.
представляет собой линию идеальных пределов мощности при различных значениях напряжения U. В частности, исходному режиму (U=100%) соответствует точка b b на этой линии.
Действительные характеристики мощности одной и той же системы электропередачи зависят от свойств приемника. Чем меньше падает напряжение приемника с ростом передаваемой мощности и угла  , тем выше действительный предел мощности, который в конце концов приблизится к идеальному пределу мощности (пунктирные кривые на рис. 81.12 и 81.13). Например, степень снижения напряжения будет уменьшаться с увеличением мощности приемной системы (местной электростанции).
, тем выше действительный предел мощности, который в конце концов приблизится к идеальному пределу мощности (пунктирные кривые на рис. 81.12 и 81.13). Например, степень снижения напряжения будет уменьшаться с увеличением мощности приемной системы (местной электростанции).
При данной мощности приемника действительный предел мощности зависит также от характеристик местных генераторов. В этом отношении уменьшение индуктивного сопротивления генераторов способствует стабилизации напряжения приемника и повышению действительного предела мощности.
Существенное влияние на ход действительной характеристики и величину действительного предела мощности оказывает так называемый регулирующий эффект нагрузки, под которым понимают степень снижения активной и реактивной мощности мощностей нагрузки при уменьшении напряжения на ее зажимах. Этот эффект принято характеризовать производными от мощностей по напряжению 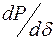 и
и 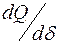 . Увеличение угла
. Увеличение угла 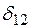 между ЭДС Е1и Е2 сопровождается, как мы убедились, снижением напряжения на шинах нагрузки. Однако с падением напряжения на шинах в какой-то мере уменьшается и мощность, потребляемая нагрузкой. Уменьшение потока мощности в сети, питающей нагрузку, в свою очередь снижает сокращает потери напряжения в генераторах, трансформаторах и линиях электропередачи и тем самым до некоторой степени как бы компенсирует падение напряжения, вызванное увеличением угла
между ЭДС Е1и Е2 сопровождается, как мы убедились, снижением напряжения на шинах нагрузки. Однако с падением напряжения на шинах в какой-то мере уменьшается и мощность, потребляемая нагрузкой. Уменьшение потока мощности в сети, питающей нагрузку, в свою очередь снижает сокращает потери напряжения в генераторах, трансформаторах и линиях электропередачи и тем самым до некоторой степени как бы компенсирует падение напряжения, вызванное увеличением угла 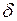 . При этом особенно
. При этом особенно 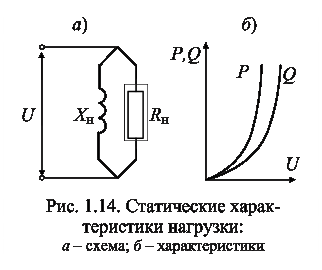 существенно влияет степень изменения реактивной мощности нагрузки, так как потери напряжения в системе с преимущественно реактивными сопротивлениями определяются прежде всего реактивными токами.
существенно влияет степень изменения реактивной мощности нагрузки, так как потери напряжения в системе с преимущественно реактивными сопротивлениями определяются прежде всего реактивными токами.
 Для учета регулирующего эффекта нагрузки необходимо знать ее статические характеристики,под которыми понимают зависимость активной и реактивной мощностей нагрузки от напряжения на ее зажимах. Касательные к статическим характеристикам нагрузки дают значения производных
Для учета регулирующего эффекта нагрузки необходимо знать ее статические характеристики,под которыми понимают зависимость активной и реактивной мощностей нагрузки от напряжения на ее зажимах. Касательные к статическим характеристикам нагрузки дают значения производных 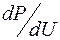 и
и 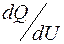 , т. е. характеристику регулирующего эффекта нагрузки. Рассмотрим статические характеристики различных видов нагрузки.
, т. е. характеристику регулирующего эффекта нагрузки. Рассмотрим статические характеристики различных видов нагрузки.
При постоянном активно-индуктивном сопротивлении нагрузки (рис. 81.14, а и б) величины активной и реактивной мощностей пропорциональны квадрату напряжения:

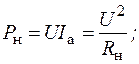
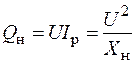 . (81.88)
. (81.88)
Регулирующий эффект такой нагрузки по активной и реактивной мощностям равен:
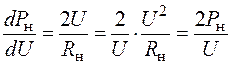 ;
;
 .
.
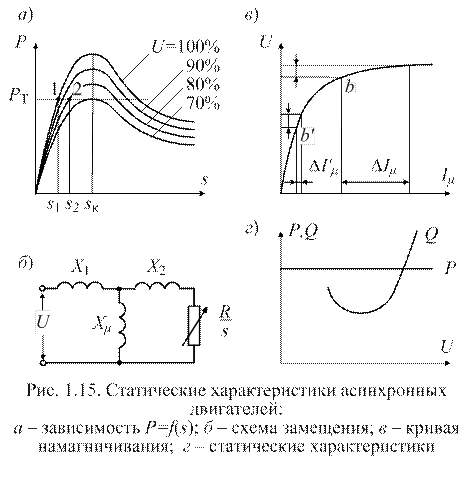
До 50% нагрузкии более составляют асинхронные двигатели.Поэтому их статистическиехарактеристики оказывают значительное влияние на статическуюустойчивость систем.Из курсаэлектрических машин и трансформаторов известна зависимость потребляемой асинхронным двигателем мощности от скольжения при различных значениях напряжения на его зажимах (рис. 81.15, а). При постоянном тормозном моменте (мощности)  уменьшение напряжения на зажимах двигателя сопровождается увеличением скольжения s до такой величины, при которой вращающий момент двигателя
уменьшение напряжения на зажимах двигателя сопровождается увеличением скольжения s до такой величины, при которой вращающий момент двигателя
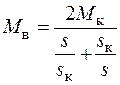
(  и
и  – критические момент и скольжение двигателя) уравновешивает тормозной момент. Например, при снижении напряжения U от 100 до 810% режим работы асинхронного двигателя переходит из точки 1 в точку 2 (рис. 81.15, а), а скольжение увеличивается от
– критические момент и скольжение двигателя) уравновешивает тормозной момент. Например, при снижении напряжения U от 100 до 810% режим работы асинхронного двигателя переходит из точки 1 в точку 2 (рис. 81.15, а), а скольжение увеличивается от  до
до 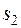 .
. 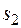 , Увеличение скольжениячто в свою очередь приводит к изменению полного сопротивления двигателя. Рассмотрим упрощенную схему замещения асинхронного
, Увеличение скольжениячто в свою очередь приводит к изменению полного сопротивления двигателя. Рассмотрим упрощенную схему замещения асинхронного
двигателя (рис. 81.15, б), на которой обозначены: 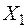 и
и 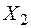 - индуктивные соротивлениясопротивления рассеяния статора и ротора, R/S – эквивалентноеРассмотрим упрощенную схемузамещения асинхронного активное двигателя (рис. 8.15, б), на которой обозначены:
- индуктивные соротивлениясопротивления рассеяния статора и ротора, R/S – эквивалентноеРассмотрим упрощенную схемузамещения асинхронного активное двигателя (рис. 8.15, б), на которой обозначены: 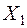 и
и 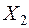 – индуктивные сопротивления рассеяния статора и ротора,
– индуктивные сопротивления рассеяния статора и ротора, 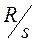 – эквивалентное активное сопротивление ротора, а
– эквивалентное активное сопротивление ротора, а 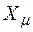 - индуктивное сопротивление намагничивания. При увеличении скольжения s падает эквивалентное активное сопротивлений сопротивление ротора
- индуктивное сопротивление намагничивания. При увеличении скольжения s падает эквивалентное активное сопротивлений сопротивление ротора 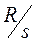 . Поэтому ток в цепи ротора
. Поэтому ток в цепи ротора 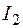 уменьшается в меньшей степени, чем в случае, когда сопро--,
уменьшается в меньшей степени, чем в случае, когда сопро--,
тивление ротора постоянно. Эти же соображения справедливы и для реактивной мощности 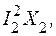 теряемой в реактивном сопротивлений сопротивлении рассеяния ротора. Следовательно, на основании изложенного регулирующий эффект асинхронного двигателя по реактивной мощности должен быть меньше, чем в рассмотренном выше случае постоянных со
теряемой в реактивном сопротивлений сопротивлении рассеяния ротора. Следовательно, на основании изложенного регулирующий эффект асинхронного двигателя по реактивной мощности должен быть меньше, чем в рассмотренном выше случае постоянных со
 |
противлений.
При определенных условиях этот эффект даже может оказаться отрицательным, когда ток 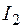 и реактивная мощность
и реактивная мощность  не уменьшаются, а увеличиваются с уменьшением напряжения на зажимах двигателя.
не уменьшаются, а увеличиваются с уменьшением напряжения на зажимах двигателя.
Однако главное влияние на регулирующийэффект асинхронногодвигателя оказывает другое обстоятельство, а именно – изменение намагничивающего тока двигателя  (рис. 81.15, в). При напряжении, близком к номинальному,асинхронный двигатель работает взоне насыщения (точка а) и небольшое снижениенапряжения
(рис. 81.15, в). При напряжении, близком к номинальному,асинхронный двигатель работает взоне насыщения (точка а) и небольшое снижениенапряжения  приводят приводит крезкому изменению намагничивающего токадвигателя
приводят приводит крезкому изменению намагничивающего токадвигателя 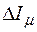 и, следовательно,потребляемой двигателем реактивноймощности. Вследствие этого регулирующийэффект асинхронного двигателяполучается даже большим, чем у цепи с постоянным сопротивлением.
и, следовательно,потребляемой двигателем реактивноймощности. Вследствие этого регулирующийэффект асинхронного двигателяполучается даже большим, чем у цепи с постоянным сопротивлением.
При низких напряжениях (точка бb) намагничивающий токменяется мало и преобладает влияние измененияэквивалентного активного сопротивления ротора 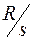 . Поэтому результирующиехарактеристикиизменениямощностиасинхронного двигателя сизменением напряжения имеют вид, показанныйна рис. 81.15,г. При неизменном тормозном моменте регулирующийэффект асинхронного двигателя по активной мощности, очевидно, равен нулю (
. Поэтому результирующиехарактеристикиизменениямощностиасинхронного двигателя сизменением напряжения имеют вид, показанныйна рис. 81.15,г. При неизменном тормозном моменте регулирующийэффект асинхронного двигателя по активной мощности, очевидно, равен нулю ( 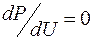 ). Регулирующий эффект по реактивной мощности
). Регулирующий эффект по реактивной мощности 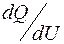 определяется касательной к статической характеристике Q=f(U). Как видно, при боль-
определяется касательной к статической характеристике Q=f(U). Как видно, при боль-
ших напряжениях он достаточно велик, затем снижается и при низких напряжениях меняет свой знак, становясь отрицательным.
 Относительно других характерных видов нагрузки можно отметить, что синхронные двигатели обладают численно небольшим регулирующим эффектом; для осветительной нагрузки эффект по реактивной мощности, естественно, равен нулю, а по активной мощности подчиняется зависимости
Относительно других характерных видов нагрузки можно отметить, что синхронные двигатели обладают численно небольшим регулирующим эффектом; для осветительной нагрузки эффект по реактивной мощности, естественно, равен нулю, а по активной мощности подчиняется зависимости 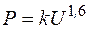 .
.
Относительно других характерных видов нагрузки можно отметить, что синхронные двигатели обладают численно небольшим регулирующим, эффектом; для осветительной нагрузки эффект по реактивной мощности, естественно, равен нулю, а по активной мощности подчиняется зависимости 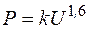 . Показатель степени 1,6 (а не 2) обусловлен изменением активного сопротивления осветительных приборовс изменением температуры нитей накала.Для печей истатических выпрямителейактивная мощность пропорциональна квадрату напряжения, т. е. они ведут себя как активное сопротивление.
. Показатель степени 1,6 (а не 2) обусловлен изменением активного сопротивления осветительных приборовс изменением температуры нитей накала.Для печей истатических выпрямителейактивная мощность пропорциональна квадрату напряжения, т. е. они ведут себя как активное сопротивление.

 В общем случае нагрузка имеет смешанный характер, поэтому да на практике часто используют статические характеристики обобщенной нагрузки, которые получают опытным путем или строят для заданного соотношения потребителей различного вида. Возможный вид статических характеристик обобщенной нагрузки показан на рис. 81.16. Очевидно, чем выше регулирующий эффект нагрузки, тем меньше деформируются характеристики мощности и тем выше действительный предел мощности (см. пунктирные кривые на рис. 81.12 и 81.13).
В общем случае нагрузка имеет смешанный характер, поэтому да на практике часто используют статические характеристики обобщенной нагрузки, которые получают опытным путем или строят для заданного соотношения потребителей различного вида. Возможный вид статических характеристик обобщенной нагрузки показан на рис. 81.16. Очевидно, чем выше регулирующий эффект нагрузки, тем меньше деформируются характеристики мощности и тем выше действительный предел мощности (см. пунктирные кривые на рис. 81.12 и 81.13).
Учет статических характеристик нагрузкаи несколько осложняет построение характеристик мощности системы и определение дейст-
вительного предела ее мощности, так как появляется необходимость в многократных электрических расчетах системы. Рассмотрим исходную систему с двумя электростанциями соизмеримой мощности (см, . рис. 81.12, а), для которой будем считать заданным исходный режим (Е10, Е20, Р10, Р20, U0). Этот режим определит даст нам первую точку характеристики мощности.
Для получения второй точки, соответствующей увеличенному значению передаваемой мощности Р11, необходимо сначала задаться некоторым новым значением активной мощности местной станций станции Р21, несколько меньшим, чем в начальном режиме. Так как при этом новом значении активной мощности местной станции Р21, уустановить однозначно изменение реактивной мощности этой станции Q2 невозможно, приходится задаваться несколькими произвольными значениями Q21(i).
Для каждого из сочетаний Р21 и Q21(i) 21(i) необходимо произвести электрический расчет системы, принимая за исходную предпосылку постоянство ЭДС Е21. Вычислив для каждого сочетания мощностей падение напряжения на генераторах местной станцийстанции, можно определять найти ряд значений напряжения на шинах приемника U1(i).1(i). При каждом данном значении напряжения активная и реактивная мощности нагрузки принимаются по ее их статическим характеристикам. Разности- мощностей нагрузки и местной станции определят поток мощностей по электропередаче. Вычислив падение напряжения на всех элементах электропередачи, получим несколько возможных значений ЭДС передающей электростанции Е11(i). 11(i). Построив кривую зависимости этой ЭДС от напряжения: приемника U (рис. 81. 17, а), по точке пересечения этой кривой с постоянным значением ЭДС генератора Е10 найдем действительный режим системы, который установится при принятом значении мощности местной станции Р21. Значения мощно 
сти передающей электростанции Р11 и напряжения U1, сооответствую
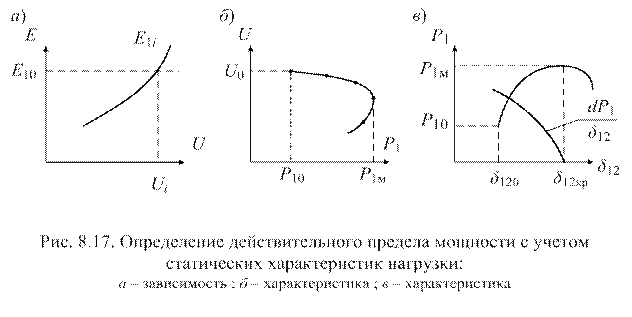
соответствующие новому режиму, дадут нам вторую точку искомой характеристики.

Задаваясь дальнейшим уменьшением мощности местной станции (Р22, Р23и т. д.) и повторяя описанные выше операции, можно получить третью, четвертую и т. д. точки характеристики мощности (рис. 81.17, 6б).
Поскольку в каждом конкретном режиме системы углы между напряжением и ЭДС  ,
, 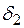 ,
, 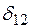 определяются однозначно (
определяются однозначно ( 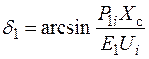 ;
;  ;
; 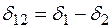 ), действительная характеристика мощности с учетом регулирующего эффекта нагрузки может быть построена и как угловая характеристика. При анализе статической устойчивости системы с двумя станциями соизмеримой мощности более удобно в качестве независимой переменной использовать не угол
), действительная характеристика мощности с учетом регулирующего эффекта нагрузки может быть построена и как угловая характеристика. При анализе статической устойчивости системы с двумя станциями соизмеримой мощности более удобно в качестве независимой переменной использовать не угол  между ЭДС передающей станции и напряжением приемника, а угол
между ЭДС передающей станции и напряжением приемника, а угол 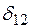 между ЭДС обеих генераторных станций (рис. 81.17, в). Максимумы характеристик мощности
между ЭДС обеих генераторных станций (рис. 81.17, в). Максимумы характеристик мощности  и
и 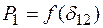 определяют действительный предел передаваемой мощности
определяют действительный предел передаваемой мощности 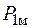 , а касательные к угловой характеристике
, а касательные к угловой характеристике 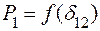 дают значения синхронизирующей мощности
дают значения синхронизирующей мощности 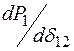 при нагрузке, заданной ее статическими характеристиками.
при нагрузке, заданной ее статическими характеристиками. 
Построение действительных характеристик и определение действительного предела мощности с учетом статических характеристик нагрузки, выполненное вышерассмотренное для условий 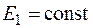 и
и 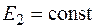 , могут может быть проведены выполнено и для случаев работы генераторов с регулированием возбуждения. В таких случаях необходимо сходите исходить из постоянства напряжения на зажимах генераторов (или ЭДС Е'), а их полную ЭДС Е определять находить аналогично тому, как это делалось в предыдущем параграфе при определении внутреннего предела мощности. Характерно, что в случае при поддержания поддержании постоянства напряжения генераторов даже при большем диапазоне изменения передаваемой мощности напряжение на нагрузке обычно изменяется незначительно,. В таком случаепоэтому можно отказаться от представления нагрузки статическими характеристиками, что существенно упрощает расчеты.
, могут может быть проведены выполнено и для случаев работы генераторов с регулированием возбуждения. В таких случаях необходимо сходите исходить из постоянства напряжения на зажимах генераторов (или ЭДС Е'), а их полную ЭДС Е определять находить аналогично тому, как это делалось в предыдущем параграфе при определении внутреннего предела мощности. Характерно, что в случае при поддержания поддержании постоянства напряжения генераторов даже при большем диапазоне изменения передаваемой мощности напряжение на нагрузке обычно изменяется незначительно,. В таком случаепоэтому можно отказаться от представления нагрузки статическими характеристиками, что существенно упрощает расчеты.
Отметим в заключение, что физика процессов, связанных со статической устойчивостью систем, и методический подход к инженерной оценке устойчивости описывались выше на примере сравнительно простых систем и в предположении, что преобладающими в системе являются, реактивные сопротивления. В действительности картина может быть значительно более сложной. Так, вВ частности, система может иметь не одну, а несколько нагрузок, ; не одну-две, а несколько генерирующих станций, ; связывающая их электрическая сеть может быть сложноэамкнутой сложнозамкнутой и т. п. В отдельных случаях необходимо учитывать не только реактивные, но и активные сопротивления элементов системы.
Анализ статической устойчивости таких систем представляет собой весьма сложную задачу. При ее решении используются известные из теоретической электротехники методы эквивалентного преобразования цепей с в целью целях упрощения схемы и принимаются дополнительные допущения, облегчающие решение задачи. Так, при большом числе генерирующих электростанций считают, что углы ЭДС всех электростанций, кроме одной, являются постоянными, активные мощности, отдаваемые всеми электростанциями, кроме двух данных, также постоянны, и т. п.
В особо сложных случаях аналитическое решение задачи статической устойчивости системы становится вообще затруднительным. Тогда, как уже отмечалось, прибегают к электронным вычислительным машинам, расчетным и физическим моделям. Однако и во всех этих сложных случаях вариантах смысл физики процессов, определяющих устойчивость системы, и подход к оценке устойчивости остаются в принципе аналогичными рассмотренным выше.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|