
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема занятия «Тригонометрические тождества»
Тема занятия «Тригонометрические тождества»
Цель занятия:формирование понятия тождества, умения доказывать тождества и упрощать тригонометрические выражения с использованием изученных формул.
1. Проверка домашнего задания и конспекта.
2. Новый материал.
Вспомним понятие тождества, тождественного выражения и тождественного преобразования. Сформулируем определения этих понятий.
Тождеством называется равенство, справедливое при всех допустимых значениях входящих в него букв.
Допустимые значения букв – это значения, которые могут принимать буквы в данном выражении.
Выражения, находящиеся в левой и правой частях тождества, называются тождественными.
Замена некоторого выражения другим, ему тождественным, называется тождественным преобразованием данного выражения.
«Зависимость между тригонометрическими функциями одного и того же аргумента».


Примеры на основные тригонометрические тождества:
Пример 1. Вычислить sin2α, если 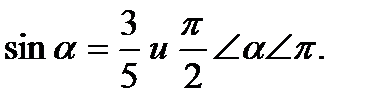
Решение. 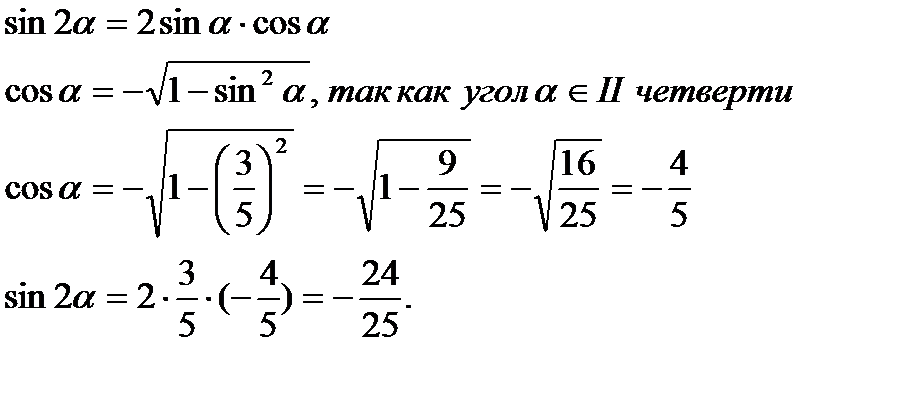
Ответ: sin2α=- 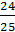
Пример 2. Найти 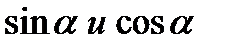 , известно, что
, известно, что 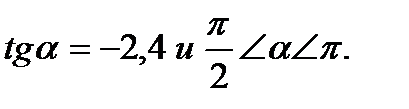
Решение. 
Для выполнения тождественных преобразований тригонометрических выражений можно использовать не только данные тригонометрические тождества, но и другие формулы тригонометрии, а также алгебраические преобразования, например, действия с дробями, вынесение за скобки общего множителя, формулы сокращённого умножения.
Тождественные преобразования используются при доказательстве тождеств. Какие вы знаете способы доказательства тождеств?
Способы доказательства тождеств:
- преобразование правой части к левой;
- преобразование левой части к правой;
- установление того, что разность между правой и левой частями равна нулю;
- преобразование левой и правой части к одному и тому же выражению.
Задача 1. Доказать, что при α ≠ πn, 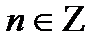 , справедливо равенство
, справедливо равенство
sin2 α + ctg2 α + cos2 α = 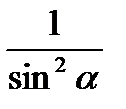
Доказательство:
sin2 α + ctg2 α + cos2 α = 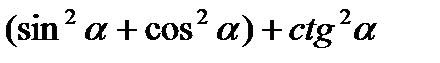 =1 + ctg2 α =
=1 + ctg2 α = 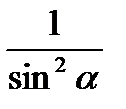
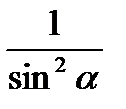 =
= 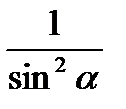 Что и требовалось доказать (Ч.т.д.)
Что и требовалось доказать (Ч.т.д.)
Задача 2. Доказать тождество cos2 α = (1 – sin α)(1 + sin α).
Доказательство:
(1 – sinα)(1 + sin α) = 1 – sin2 α = cos2 α
cos2α = cos2α Ч.т.д.
Задача 3. Доказать тождество:
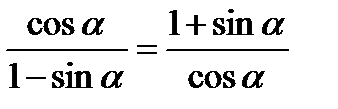
Доказательство:
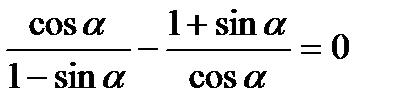
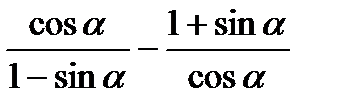 =
= 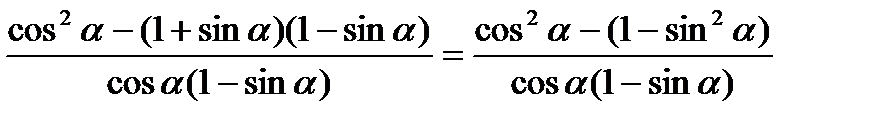 =
=
= 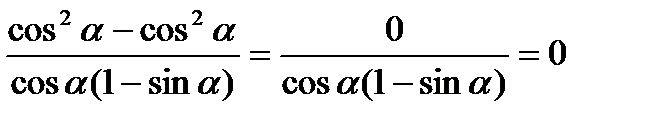
0=0. Ч.т.д.
Задача 4. Доказать тождество:
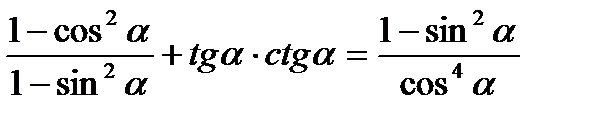
Доказательство:
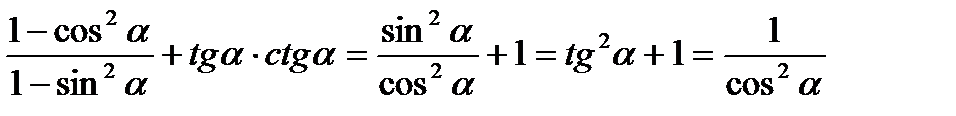
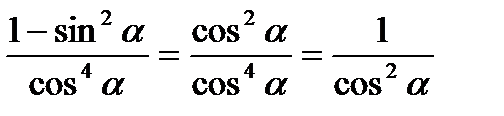
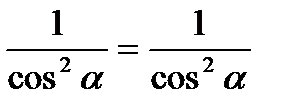 Ч.т.д.
Ч.т.д.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|