
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание: законспектировать решённые в информационной карте примеры и выполнить домашнее задание.
Задание: законспектировать решённые в информационной карте примеры и выполнить домашнее задание.
Информационная карта
Тема урока: Рациональные уравнения.
Цель: научиться решать рациональные системы уравнений.
Ход урока:
Системы рациональных уравнений.
1).Способ подстановки.
ПРИМЕР 1. Решим систему уравнений 
Выразив у через х из первого уравнения системы, получим уравнение:
у = 3х - 1.
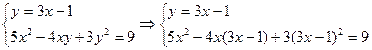
Решив уравнение 5x2-4(3x-1)+3(3x-1)2=9, найдем его корни х1 = 1 и х2 = 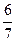 . Подставив найденные числа х1 и х2 в уравнение у = 3х - 1 , получим у1 = 2
. Подставив найденные числа х1 и х2 в уравнение у = 3х - 1 , получим у1 = 2
и у =  Следовательно, система имеет два решения: (1; 2) и (
Следовательно, система имеет два решения: (1; 2) и ( 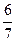 ;
;  )
)
Ответ. (1; 2), ( 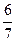 ;
;  )
)
2).Метод алгебраического сложения.
ПРИМЕР 2. Решим систему уравнений 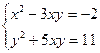
Оставив без изменения первое уравнение системы и сложив первое уравнение со вторым, получим систему равносильную системе.
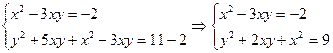
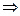
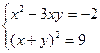
Все решения системы есть объединение всех решений двух систем: 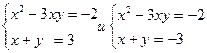
Решив каждую из этих систем, найдем все решения системы (2; 1), (-2; -1), 
Ответ. (2; 1), (-2; -1),  .
.
3).Метод введение новых неизвестных.
ПРИМЕР 3. Решим систему уравнений 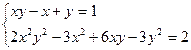
Обозначив u = ху, v = х - у, перепишем систему в виде 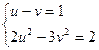
Найдем ее решения: u1= 1, v1 = 0 и u2 = 5, v2 = 4. Следовательно, все решения системы есть объединение всех решений двух систем:
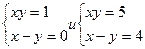
Решив методом подстановки каждую из этих систем, найдем ее решения системы: (1; 1), (-1; -1), (5; 1), (-1; -5).
Ответ. (1; 1), (-1; -1), (5; 1), (-1; -5).
4). Уравнение вида ах2+ bху + су2 = 0, где а, b, с — данные неравные нулю числа, называют однородным уравнением относительно неизвестных х и у.
Рассмотрим систему уравнений, в котором есть однородное уравнение.
ПРИМЕР 4. Решим систему уравнений 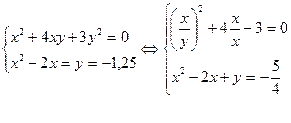
Обозначив t = 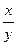 , перепишем первое уравнение системы в виде t2+4t+3=0.
, перепишем первое уравнение системы в виде t2+4t+3=0.
Уравнение имеет два корня t1 = -1 и t2 = -3, поэтому все решения системы есть объединение всех решений двух систем:
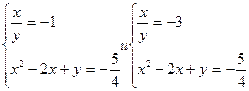
Решив каждую из этих систем, найдем все решения системы: (2,5; -2,5), (0,5; -0,5), 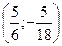 ,(1,5;-0,5). Ответ. (2,5; -2,5), (0,5; -0,5),
,(1,5;-0,5). Ответ. (2,5; -2,5), (0,5; -0,5), 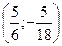 ,(1,5;-0,5).
,(1,5;-0,5).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|