Контакты

Случайная статья

Решение показательных и логарифмических уравнений.

Стр 1 из 2Следующая ⇒

Решение показательных и логарифмических уравнений.

При решении показательных уравнений необходимо помнить, что решение любого показательного уравнения сводится к решению “простейших” показательных уравнений, то есть уравнений вида: 1) a^f(x)= a^g(x) или 2) a^f(x)= b.

Очевидно, что уравнение типа 2 сводится к уравнению типа 1 с помощью основного логарифмического тождества: 3 a^f(x)= .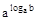

Уравнение (1) равносильно уравнению f(x) = g(x) при а > 0, а ¹ 1.

1. Решить показательное уравнение

а) .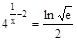

Решение: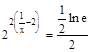; ; 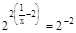; ; 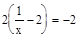; 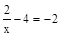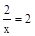x=1.

Проверка: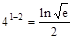; ; 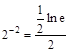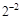=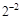– верно.

Ответ: х=1;

б) .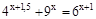

Решение: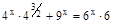; . Разделим обе части данного уравнения на 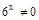. 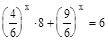; 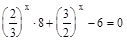. Пусть , тогда уравнение примет вид: ; , ; ; ;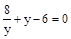

; .

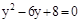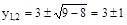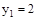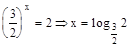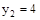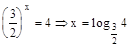Проверка: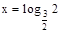; 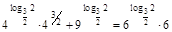. Делим на .

; ; ;

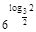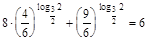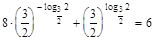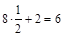6=6 – верно;

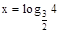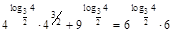; . Делим на ;

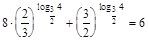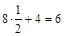; ; 6=6 – верно.

Ответ: ; .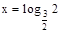

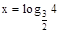в) 5^3х – 2 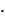5^{3х -1} – 3 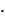5^{3х – 2} = 60

Решение

5^3х - 2 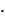5^{3х -1} - 3 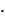5^{3х – 2} = 60,

Уравнение решается методов вынесения общего множителя за скобки

5^3х (1-2 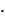5^-1 - 3 5^{– 2} ) = 60,

5^3х 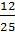= 60, разделим обе части уравнения на дробь 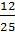, получаем

5^3х = 125,

3х =3,

х=1.

Ответ: х=1.

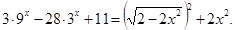г)

Решение

т.к.

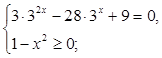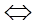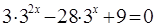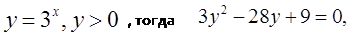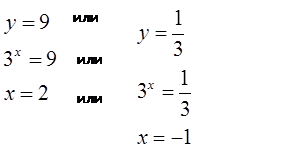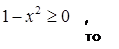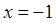Ответ:-1.

2. Решить логарифмическое уравнение:

а)log_x_–19 = 2.

Решение. Данное уравнение равносильно системе

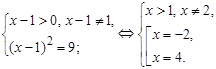
Ответ. x = 4.

б) 3²^log4 ^x⁺²=16x².

Решение. Область определения x >0. Прологарифмируем обе части по основанию 4.

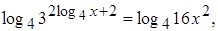
Используя свойства логарифмов, получим

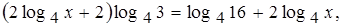
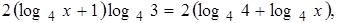
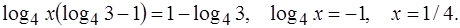
Ответ x = 1/4

в)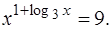

Решение.Область определения уравнения х > 0. Так как при х > 0 обе части уравнения положительны, а функция y = log₃t монотонна, то

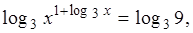
(1 + log₃x) log₃x = 2.

Введём новую переменную t, где t = log₃x, tÎR.

(1 + t) t = 2, t² + t – 2 = 0, t₁= –2, t₂= 1.

log₃x = –2 или log₃x = 1,

x = 1/9 или х = 3.

Ответ. х = 1/9; х = 3.

г)

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.